Oberstufe
W.18 | Normalverteilung
Die Mehrzahl der zufälligen Ereignisse im Universum sind normalverteilt. Diese Verteilung wird durch eine Funktion beschrieben, durch die Gauß´sche Glockenkurve (das ist nichts Anzügliches). Das Schöne daran ist, dass man (um diese Funktion aufzustellen) nur den Erwartungswert und die Standardabweichung braucht. Man verwendet die Normalverteilung nur bei stetigen Ereignissen (d.h. beliebige Kommazahlen müssen Sinn ergeben). Leider hat die Normalverteilung den Nachteil, dass man auf rechnerischem Weg recht schwer zur Wahrscheinlichkeit kommt. Daher verwendet man Tabellen dazu. Die Hauptanwendung der Normalverteilung in Schule und Studium ist wohl die „Umwandlung“ der Binomialverteilung in die Normalverteilung (Unterkapitel W.18.03 „Näherungsformel von Moivre-Laplace“)
Es gibt zwei ganz wichtige Verteilungen in der Wahrscheinlichkeitsrechnung:
die Binomialverteilung und die Normalverteilung
Für Schule/Studium ist die Binomialverteilung vermutlich die einfachere aber wichtigere von allen. Die Normalverteilung betrachten wir im übernächsten Kapitel [W.18]. Auf Gemeinsamkeiten und Unterschiede zwischen beiden Verteilungen gehen wir im Kapitel W.18.03 ein [„Laplace-Bedingung“].
Die Normalverteilung [oder auch Gauß-Verteilung] wendet man an
- wenn es um eine stetige Verteilung geht, d.h. wenn jede beliebige Kommazahl vorkommen kann [→Beispiel a.] oder auch
- wenn z.B. bei einer „normalen“ Binomialverteilung die Zahlen so groß sind, dass die Taschenrechner [bzw. Computer] versagen [→Beispiel e.].
W.18.01 | Allgemeines
Erst ein bisschen Blablah:
Die Normalverteilung geht auf Carl Friedrich Gauß zurück [DAS Tier unter den Mathematikern schlechthin]. Auch wenn Ihnen das aus Sicht eines Schülers oder Studenten vielleicht seltsam vorkommen mag, so ist die Normalverteilung eigentlich die wichtigste Verteilung der Wahrscheinlichkeitsrechnung.
Zum einen liegt das daran, dass fast alle zufälligen Ereignisse des Universums durch die Normalverteilung beschreiben lassen, zum anderen liegt das daran, dass sich fast jede andere Verteilung aus der Wahrscheinlichkeitstheorie der Normalverteilung annähert [zumindest wenn die Anzahl der betrachteten Ereignisse groß wird].
Auf den ersten Blick sieht die Normalverteilung furchtbar aus. Die Formel der Normalverteilung sieht furchtbar aus und um Rechnungen mit der Normalverteilung durchzuführen, müsste man eigentlich Integrale lösen, die mathematisch gar nicht lösbar sind.
Um das zu in den Griff zu kriegen, geht man zwei Umwege: zum einen standarisiert man alle Normalverteilungen [Kapitel W.18.02] und man verwendet danach eine Tabelle.
Letztendlich muss man sich nur ein bisschen an diese Standarisierung und an die Verwendung der Tabelle gewöhnen, dann werden plötzlich alle Rechnungen mit der Normalverteilung einfach.
Die Kurve der Normalverteilung wird über eine Funktion beschrieben, die Dichtefunktion der Normalverteilung heißt oder Gauß´sche Glockenkurve.
[gut möglich, dass es noch andere Namen dafür gibt].
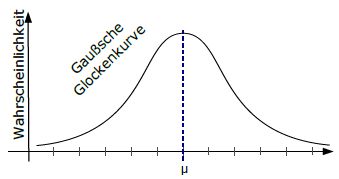
Die höchste W.S. ist immer beim Mittelwert μ, nach außen hin nimmt die W.S. dann gegen Null ab.
Die gezeichnete Kurve wird durch folgende Funktion beschrieben:

p(x) ist die W.S.
μ ist der Erwartungswert
σ ist die Standardabweichung
Wie berechnet man nun mit dieser Funktion Wahrscheinlichkeiten?
Man kann mit der Normalverteilung immer nur eine W.S. von einem Intervall berechnen [also die W.S. von … bis …] und dafür braucht man das Integral von p(x). Die Intervallgrenzen sind dabei die Integralgrenzen. [→Beispiel a.]

Häufig verwendet man Intervalle, die genau eine, zwei oder drei Standarabweichungen um den Mittelwert liegen, denn da hat die Normalverteilung eine nette Eigenschaft:
- Alle Werte, die maximal eine Standardabweichung vom Mittelwert abweichen, haben eine Häufigkeit von ca. 68,3%.

- Alle Werte, die maximal zwei Standardabweichungen vom Mittelwert abweichen, haben eine Häufigkeit von ca. 95,4%.
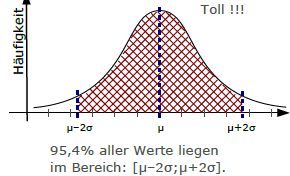
- Alle Werte, die maximal drei Standardabweichungen vom Mittelwert abweichen, haben eine Häufigkeit von ca. 99,7%.
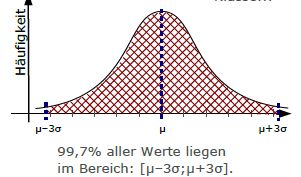
Diese Intervalle nennt man „Sigma-Intervalle“ und wir sehen in Beispiel b. wie man das geschickt verwenden kann.

Beispiel a.

Die durchschnittlichen Augusttemperatur in Usbekistan liegt bei 25,5°C. Als Varianz wird 40 angegeben.
Mit welcher W.S. zeigt eine zufällig durchgeführte Temperaturmessung 28°C an?
Lösung:
Zuerst was Grundsätzliches zur Normalverteilung:
Die W.S., dass eine Temperatur bei haargenau bei 28°C liegt, beträgt natürlich Null, denn wir reden in Mathe üblicherweise davon, dass unendlich viele Nachkommastellen stimmen. Im Alltag interessieren mich natürlich nicht unendlich viele Nachkommastellen der Temperatur. Wenn die Temperatur mit auf ganze Zahlen gerundet ist, meint man also eine Temperatur, die zwischen 27,5° und 28,5° liegt!
Das wird mit dem Integral der Formel p(x) berechnet, wobei 27,5 und 28,5 die Grenzen sind.
μ = 25.5
σ² = Var = 40
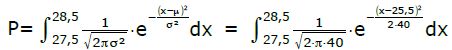
Dummerweise kann man dieses Integral von Hand gar nicht berechnen. [Probieren Sie´s erst gar nicht. Sie würden entweder versagen oder sich verrechnen, also ersparen Sie sich die Blamage!]
Das Integral kann nur mit einem Computerprogrammoder mit einem GTR oder CAS berechnet werden.
Man erhält ein Ergebnis von 0,058 = 0,58%
Die Berechnung erfolgt üblicherweise anders. →Beispiel d.
Leider werden Sie diesen Rechenweg (vermutlich) nie brauchen werden.
Beispiel b.

In Tadschikistan verbraucht jeder Haushalt jährlich 115 Rollen Klopapier. Die Standardabweichung des Verbrauchs wird von dem nationalen Klopapierverbrauchkomitee mit 27 Rollen angegeben.
Wieviel Rollen Klopapier verbraucht ungefähr das eine Prozent der Bevölkerung mit dem ungewöhnlichsten Verbrauchsverhalten?
Lösung:
Es gibt für die Normalverteilung drei Intervalle, für die sehr, sehr einfache Rechnungen möglich sind.
Im 1σ-Intervall befinden sich ca. 68,3% aller möglichen Fälle [also rund zwei Drittel],
im 2σ-Intervall befinden sich ca, 95,4% aller möglichen Fälle,
im 3σ-Intervall befinden sich ca. 99% aller möglichen Fälle [eigentlich 99,7%].
[Das 1σ-Intervall ist dabei das Intervall, das vom Mittelwert maximal eine Standardabweichung nach unten oder nach oben abweicht, vergleichbar sind auch das 2σ-Intervall und das 3σ-Intervall definiert.]
In dieser Aufgabe verwenden wir das 3σ-Intervall, denn „1% mit dem ungewöhnlichsten Verhalten“ bedeutet „1% der seltensten Fälle“ was wiederum das Gegenteil der „99% der häufigsten Fälle“ ist. Das 3σ-Intervall hat zwar eine Größe von 99,7%, nicht 99%, über diesen Rundungfehler sehen wie jedoch hinweg,
Nun aber der Reihe nach.
Wenn der Mittelwert bei μ=115 Rollen liegt und die Standardabweichung bei σ=27, so beträgt das 3σ-Intervall: [μ–3σ;μ+3σ] = [115–3·27;115+3·27] = [34;196].
Das bedeutet also, dass diejenigen 99% der Tadschiken, die den normalsten Klopapierverbrauch haben, zwischen 34 und 196 Rollen Klopapier verbrauchen.
Diejenigen, die das seltenste [bzw. ungewöhnlichste] Verhalten aufweisen, verbrauchen weniger als 34 oder mehr als 196 Rollen. [Diese Haushalte machen insgesamt 1% aus.]

In Kirgistan regnet es monatlich 25 Liter [keine Ahnung, ob´s tatsächlich stimmt].
In zwei Drittel aller Monate liegt die Regenmenge zwischen 16,6 und 33,4 Liter.
In welchem Bereich liegt die Regenmenge, die in 95% aller Fälle fällt?
Lösung:
Uns ist der Mittelwert gegeben, aber nicht die Standardabweichung.
Die Standardwege der Normalverteilung [die wir später manchen werden], funktionieren selbstverständlich alle. Die sind aber zu kompliziert.
Entscheidend ist nämlich, dass die Intervalle eine Größe haben, die genau die den Sigma-Intervallen entsprechen.
Das 1σ-Intervall hat eine Größe von 68% [das sind zwar nicht genau zwei Drittel, aber annähernd]. Das bedeutet, dass von 25 bis 16,6 bzw. von 25 bis 33,4 jeweils ein σ lang ist. ⇒ 1σ=25–16,6[=33,4–25]=8,4.
Zufällig hat das 2σ-Intervall eine Größe von 95%. Und da ja die Regenmenge gefragt ist, die in 95% aller Fälle auftritt, ist genau dieses 2σ-Intervall gefragt.
Das 2σ-Intervall ist: [μ–2·σ; μ+2·σ] = [25–2·8,4;25+2·8,4] = [ 8,2 ; 41,8].
In 95% aller Fälle liegt die monatliche Regenmenge in Kirgistan zwischen 8,2 und 41,8 Litern. Das ist schön für Kirgistan.
W.18.02 | Standard-Normal-Verteilung
Da die Normalverteilung eine sehr wichtige Verteilung ist, die Rechnungen [wie wir im letzten Kapitel gesehen haben] von der Schwierigkeit her, nur für wenige Sonderfälle akzeptabel sind, wurde eine bessere Rechen-Möglichkeit entwickelt.
Das ist die Standard-Normal-Verteilung, kurz SNV.
Man betrachtet eine ganz bestimmte Normalverteilung, nämlich die mit dem Mittelwert μ=0 und der Standardabweichung σ=1. Man nennt diese
Normalverteilung: „Standard-Normal-Verteilung“.
Von dieser SNV gibt es für jede notwendige Rechnung eine ausführliche Tabelle.
Alle anderen Normal-Verteilungen des Universums führt man mittels einer einfachen Formel auf diese eine SNV zurück.
|
Die Standard-Normal-Verteilung hat den Mittelwert μ=0 und die Standardabweichung σ = 1 |
Wie funktioniert das im Detail?
Man rechnet jeden Wert einer üblichen Normalverteilung in den zugehörigen Wert der Standard-Normal-Verteilung um.
Einen Wert einer beliebigen Normalverteilung bezeichnet man immer mit „x“.
Einen Wert der Standard-Normal-Verteilung bezeichnet man immer mit „z“.
Die Formel für die Umrechnung lautet:

μ und σ sind Mittelwert und Standardabweichung der ursprünglichen Normalverteilung.
Hat man „z“ errechnet, schlägt man in der Tabelle die zugehörige W.S. nach.
Beispiel d.

Die durchschnittlichen Augusttemperatur in Usbekistan liegt bei 25,5°C.
Als Varianz wird 40 angegeben.
Mit welcher W.S. zeigt eine zufällig durchgeführte Temperaturmessung 28°C an?
Lösung:
Der gegebene Mittelwert liegt bei μ=25,5, die Standardabweichung ist die Wurzel aus der Varianz, 
Natürlich kann man nicht die W.S. von einer einzigen Zahl berechnen, die W.S., dass die Temperatur bei genau 28° liegt [also auf unendlich viele Nachkommastellen genau], ist Null. Wenn man im Alltag von 28° spricht, ist das der gerundete Wert für das Intervall, dass bei 27,5° beginnt und bei 28,5° endet. Es geht also primär um die Werte x1=27,5 und x2=28,5.
Diese Werte rechnen wir in die zugehörigen Werte der Standard-Normal-Verteilung um [diese Werte heißen „z“]. Dafür verwenden wir die tolle Formel.

Nun schnappt man sich die Tabelle für die Werte der SNV [siehe Ende des Kapitels] und schlägt die W.S. für die Werte z1 und z2 nach.
z1=0,32 ⇒ Φ1=0,6255 z2=0,47 ⇒ Φ2=0,6808
Die Differenz von Φ1 und Φ2 ist die gesuchte W.S. [ohne Begründung, warum das so ist].
P(ca. 28°) = 0,6808–0,6255 = 0,0553 = 5,53%.
Beispiel e.

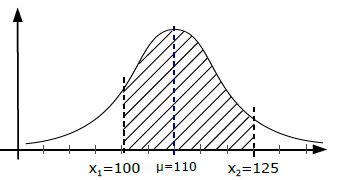
Bei einem Gewinnspiel, bei welchem üblicherweise 55% Frauen teilnehmen, werden 200 Preise ausgelost.
Wie hoch ist die WS., dass sich unter den Gewinnern mindestens 100 aber höchstens 125 Frauen befinden?
Lösung:
Normalerweise könnte man diese Aufgabe über Binomialverteilung rechnen. Wenn Sie allerdings versuchen die Rechnung in den Taschenrechner einzutippen, wird der Taschenrechner wegen zu hohen Zahlen streiken.
[Manche neuere Taschenrechnermodelle können das zwar rechnen, aber intern rechnen die dann ebenfalls über die Normalverteilung, nicht über Binomialverteilung]. Wir müssen deswegen für die Rechnung den Weg über die Standard-Normal-Verteilung gehen.
Was wissen wir? Wir errechnen μ und σ über die Formeln der Binomialverteilung.
μ = n·p = 200·0,55 = 110.
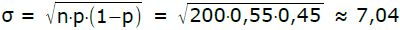
Da σ>3, darf man statt der Binomialverteilung die SNV anwenden [→Kapitel W.18.03]
Nun rechnet man die x-Werte der Binomialverteilung in die z-Werte der SNV um.
[Da die Binomialverteilung nur ganze Zahlen kennt, die Normalverteilung aber mit Kommazahlen arbeitet, muss man bei der Umrechnung immer noch den Korrekturfaktor „0,5“ in die Formel mit einbringen. Beim größeren x-Wert zählt man „0,5“ dazu, beim kleineren x-Wert zieht man „0,5“ ab!]

Nun schlägt man in der Tabelle die Werte der Phi-Funktion nach [siehe Ende des Kapitels] und erhält Φ1 und Φ2 [Φ ist die W.S. in der SNV].
z1=-1,49 ⇒ Φ(-1,49) = 1–Φ(1,49) = 1–0,9319 = 0,0681
z2=2,20 ⇒ Φ(2,20) = 0,9861
Die Differenz von Φ1 und Φ2 ist die gesuchte W.S.
⇒ P(100?X?125) = Φ2–Φ1 = 0,9861–0,0681 = 0,918
Antwort: Die W.S., dass mindestens 100, aber höchstens 125 Frauen unter den Gewinnern sind, liegt bei 0,918 ? 91,8%.
Beispiel f.
Bei einem Gewinnspiel, werden 200 Preise ausgelost, wovon 110 an Frauen gehen. Wie hoch ist die W.S., dass sich unter 60 ausgewählten Personen mindestens 42 aber höchstens 45 Frauen dabei sind?
Lösung:
Dieses ist weder eine Binomialverteilung, noch eine Normalverteilung, da sich die W.S. bei jedem „Zug“ ändert. Es handelt sich um eine hypergeometrische
Verteilung [→Kapitel W.17]. Die korrekte Lösung wäre:

Beispiel g.

Eine Firma stellt rosa Klobürsten her. Für eine Werbeaktion wird jede zwölfte Bürste im Farbton „kackbraun“ produziert.
Mit welcher W.S. sind unter 1000 Klobürsten mindestens 100 kackbraune dabei?
Lösung:
Wir haben hier eine klassische Binomialverteilung.
Da es jedoch sehr viele Möglichkeiten gibt [100 bis 1000 kackbraune Bürsten] und die Zahlen zudem sehr hoch sind, ist der Weg über SNV empfehlenswert.

Wir berechnen zuerst Mittelwert und Streuung:

[Da σ>3, ist die Umrechnung von Binomialverteilung in SNV erlaubt →Kapitel W.18.03].
Nun haben wir ein weiteres kleineres Problem: normalerweise braucht man für die SNV zwei Grenzen. Hier haben wir nur einen x-Wert [der nur einen z-Wert liefern wird].
Das stimmt natürlich nicht ganz, wir haben einen zweiten x-Wert.
Da die Frage nach „mindestens 100“ Klobürsten gestellt wurde, ist die untere Grenze „100“, die obere Grenze ist dabei „1000“ [man könnte auch ∞ als obere Grenze nehmen].

[Den Korrekturwert „0,5“ braucht man immer bei der Umwandlung einer Binomialverteilung in die SNV. Beim höheren z-Wert zählt man „0,5“ dazu, beim kleineren z-Wert zieht man „0,5“ ab.]
Aus der Tabelle entnehmen wir die zugehörigen W.S.
z1=1,85 ⇒ Φ(1,85) = 0,9678
z2=103,8 ⇒ Φ(103,8) = 1 [in der Tabelle liefern alle Werte ab z=3,9 die W.S. Φ=1]
Die Differenz von Φ1 und Φ2 ist die gesuchte W.S.
⇒ P(X?100) = Φ2–Φ1 = 1–0,9678 = 0,0322
Antwort: Die W.S., dass mindestens 100 kackbraune Klobürsten dabei sind, liegt bei ca. 0,032 ? 3,2%.
Beispiel h.
Ein Glücksrad ist in drei gleiche Sektoren eingeteilt, welche die Felder Apfel, Birne und Kirsche zeigen. Im Laufe seiner Existenz wird das Glücksrad voraussichtlich 600.000 mal gedreht. Mit welcher W.S. zeigt das Glücksrad eine „Apfel-Häufigkeit“, die um mindestens 1.000 vom Erwartungswert abweicht?
Lösung:
Da das Glücksrad in drei gleiche Sektoren eingeteilt ist, ist die W.S. [pro Drehung!] für jeden Sektor jeweils 
Der Mittelwert für „Apfel“ liegt also bei: 
Wenn die Apfel-Häufigkeit um mindestens 1000 vom Mittelwert abweicht, so sollte also eine Häufigkeit auftreten, die kleiner als 199.000 ist oder größer als 201.000.
Die beiden Grenzen sind also x1=197000 und x2=203000.
Um die zugehörigen z-Werte zu berechnen, brauchen wir die Standardabweichung.

[Da σ>3, ist die Umrechnung von Binomialverteilung in SNV erlaubt →Kapitel W.18.03].

[Den Korrekturwert „0,5“ braucht man immer bei der Umwandlung einer Binomialverteilung in die SNV. Beim höheren z-Wert zählt man „0,5“ dazu, beim kleineren z-Wert zieht man „0,5“ ab.]
Aus der Tabelle entnehmen wir die zugehörigen W.S.
z1=-2,74 ⇒ Φ(-2,74) = 1–Φ(2,74) = 1–0,9969 = 0,0031
z2=2,74 ⇒ Φ(2,74) = 0,9969
Jetzt gibt es aber noch ein kleines Problem:
Die Differenz der beiden W.S.-Werte liefert in der SNV immer die W.S. zwischen x1 und x2.
Wir brauchen aber die W.S. außerhalb der x-Werte.
Wir bestimmen zuerst die W.S. zwischen den x-Werten: P(199000?X?201000) = 0,9969–0,0031 = 0,9938
Die W.S., dass weniger als 199000 mal oder öfter als 201000 mal „Apfel“ angezeigt wird, ist das Gegenereignis.
P(X?199000 oder X?201000) = 1–0,9938 = 0,0062
Antwort: Die W.S., dass die Apfel-Häufigkeit um mindestens 1000 vom Erwartungswert abweicht, liegt bei ca. 0,0062 ? 0,62%.
W.18.03 | Näherungsformel von Moivre-Laplace
Die Laplace-Bedingung brauchen Sie, wenn Sie die Binomialverteilung und die Normalverteilung [=Gaußverteilung] beherrschen müssen.
Erläuterung:
Die Binomialverteilung und die Normalverteilung sind zwei sehr sehr ähnliche Verteilungen. Für hohe Stückzahlen ist es sogar so, dass die Unterschiede vernachlässigbar sind.
[Am Ende des Kapitels gehen wir kurz auf die Unterschiede zwischen beiden Verteilungen ein].
Die Laplace-Bedingung sagt nun aus, unter welchen Umständen die Unterschiede zwischen beiden Verteilungen vernachlässigbar sind:
|
Wenn die Standardabweichung größer als drei ist ( σ>3 ), |
Beispiel i.
Ein idealer Würfel wird 50 mal geworfen. Es soll geprüft werden, mit welcher W.S. die „5“ neun Mal fällt. Prüfen Sie, ob diese Fragestellung über die Normalverteilung beantwortet werden darf.
Lösung:
Man darf statt der Binomialverteilung die Normalverteilung verwenden, wenn die Standardabweichung mindestens 3 beträgt. Also berechnen wir σ.
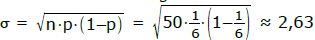
Die Normalverteilung darf nicht verwendet werden!
Beispiel j.
Ein idealer Würfel wird 50 mal geworfen. Es soll geprüft werden, mit welcher W.S. neun Mal die „5“ oder „6“ fällt. Prüfen Sie, ob diese Fragestellung über die Normalverteilung beantwortet werden darf.
Lösung:
Die W.S., dass die „5“ oder „6“ fällt, liegt bei p= 2/6 pro Wurf.
Man darf statt der Binomialverteilung die Normalverteilung verwenden, wenn die Standardabweichung mindestens 3 beträgt. Also berechnen wir σ.
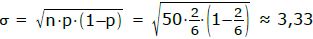
Man dürfte hier nach Belieben die Binomial- oder die Normalverteilung darf anwenden!
Beispiel k.
Ein idealer Würfel wird 5000 mal geworfen. Es soll geprüft werden, mit welcher W.S. die „5“ mindestens 900 Mal fällt. Prüfen Sie, ob diese Fragestellung über die Normalverteilung beantwortet werden darf.
Lösung:
Selbstverständlich darf die Normalverteilung verwendet werden, denn die Zahlen sind so hoch, dass die Standardabweichung mit Sicherheit über 3 liegt.

In dieser Aufgabe ist es sogar so, dass man die Normalverteilung anwenden muss, denn die auftretenden Zahlen sind zu hoch für einen Taschenrechner. Wenn Sie die Aufgabe über die Binomialverteilung rechnen wollten, müssten Sie ja z.B. irgendwann mal den Binomialkoeffizient  eintippen. Bei diesen Riesenzahlen streikt jeder Taschenrechner. Sie müssen also den Weg über Normalverteilung gehen!
eintippen. Bei diesen Riesenzahlen streikt jeder Taschenrechner. Sie müssen also den Weg über Normalverteilung gehen!
[Bemerkung: Falls Sie über einen GTR/CAS verfügen, bei dem man die Binomialverteilung direkt eingeben kann: diese Taschenrechner verwenden klammheimlich auch die Normalverteilung]
Unterschied zwischen Binomial- und Normalverteilung
Der wichtigste Unterschied zwischen der Binomialverteilung und der Normalverteilung [= Gaußsche Glockenkurve = Gaußverteilung] ist der, dass die Binomialverteilung nur für ganzzahlige Werte existiert und die Normalverteilung für alle beliebigen Kommazahlen. Mathematisch formulieren Sie das so: die Binomialverteilung ist eine „diskrete“ Verteilung, die Normalverteilung ist „stetig“.
Deswegen gibt´s von der Binomialverteilung auch keine Kurve, sondern nur ein Balkendiagramm (=Histogramm) [da ja nur ganze Zahlen als x-Wert eingesetzt werden können, keine Kommazahlen].
Die Normalverteilung wird durch eine schöne Kurve beschrieben, da [wie gesagt] jede beliebige Zahl als x-Wert eingesetzt werden kann [und einen y-Wert liefert].
Bei einer Binomialverteilung kann man die W.S. für eine Zahl berechnen [man kann z.B. die W.S. dafür berechnen genau eine rote Kugel aus einer Urne zu ziehen].
Bei einer Normalverteilung kann man nicht die W.S. für genau eine Zahl berechnen.
[Mit welcher W.S. trifft ein Schütze genau 2cm neben das Ziel? Antwort: mit einer W.S. von 0, denn 2cm heißt in Mathe 2,0000... cm (also unendlich viele Nachkommastellen genau) und nicht einmal einen Atomdurchmesser daneben]. Man kann bei der Normalverteilung also nur W.S. für Intervalle berechnen [bei unserem Bsp. mit dem Schützen hieße das, dass wir die 2cm Abweichung runden, also berechnen wir die W.S., dass die Abweichung z.B. zwischen 1,5cm und 2,5cm liegt]. Die Abweichung von einem Intervall kann man nur über ein Integral berechnen [die Integralgrenzen sind dann die Grenzen des Intervalls] oder aus der Tabelle der Normalverteilung ablesen.
Tabellenwerte der Standard-Normal-Verteilung [=Phi-Funktion]
Die Tabelle gibt es hier zum Download.
Wie liest man diese Tabelle?
Die linke Spalte [fettgedruckt] gibt den „z“-Wert bis auf die erste Nachkommastelle an, die Spalten weiter rechts zeigen die zweite Nachkommastelle an. Z.B. gehört zum Wert z=2,97 die Wahrscheinlichkeit ?=0,9985, die in der Zeile „2,9“ und in der Spalte „0,07“ steht.
Die Wahrscheinlichkeit von negativen „z“-Werten ist die Differenz bis 1. Zu z=-2,97 gehört also die W.S. ?=1–0,9985=0,0015.
Die angegebene W.S. ist immer die W.S., dass höchstens der gesuchte Wert auftritt, also die W.S. von -∞ bis z.
Details zum genauen Umgang mit der Tabelle finden Sie in Kapitel „W.18.02“.


