Oberstufe
A.15 | Tangenten und Normale
Eine Tangente ist eine Gerade, die eine Funktion in einem bestimmten Punkt berührt. Die Steigung von Tangenten ist die Ableitung der Funktion, in welche der x-Wert des Berührpunktes eingesetzt werden muss. Eine Normale steht senkrecht (orthogonal) auf der Tangente und ist damit eine Lotgerade der Tangente bzw. der Normalen. Die Steigung der Normalen ist der negative Kehrwert der Tangentensteigung (m1=-1/m2). Man sagt dazu auch: Die beiden Steigungen sind negativ reziprok.
Es gibt mehrere Methoden Tangenten und Normale zu berechnen.
Ich werde hier zwei Methoden vorstellen, mit denen das geht.
⇒ Die gängigste ist die Methode ist die über y=mx+b
⇒ Die geschickteste Methode ist über die Tangenten- bzw. Normalenformel
⇒ Es gibt eine dritte Methode, die über die Punkt-Steigungs-Formel geht, diese ähnelt aber dem Weg über Tangenten- und Normalengleichung. Ich stelle diese Methode daher hier nicht vor.
Mit der ersten Methode kann man fast alle Tangentenaufgaben lösen.
Mit der zweiten Methode kriegt man alle Fragestellungen zu Tangenten hin.
Was ist überhaupt eine Tangente oder eine Normale?
Eine Tangente ist eine Gerade, die eine Funktion in einem bestimmten Punkt [dem Berührpunkt] berührt.
Eine Normale ist eine Gerade, die in einem bestimmten Punkt [dem Berührpunkt der Tangente] senkrecht auf der Tangente steht.
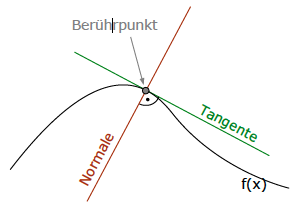
Das Wichtigste bei der Berechnung von Tangenten ist, zu wissen, dass man die Tangentensteigung über die erste Ableitung berechnet.
Es gilt: mTan = f'(u) Hierbei ist „u“ der x-Wert des Berührpunktes.
Aus der Tangentensteigung kann man die Normalensteigung berechnen [falls man die braucht].
Die Normalensteigung ist der negative Kehrwert der Tangentensteigung. Es gilt: 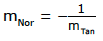

[A.15.01] Methode 1: Tangente und Normale berechnen über y=mx+b
Beispiel a.
Sei f(x) = x³+5x²+6x
Bestimmen Sie die Gleichung der Tangente und der Normalen an f(x) im Punkt B(-1|f(-1)) !
Lösung:
Erstmal rechnen wir B vollständig aus.
f(-1) = (-1)3 + 5·(-1)2 + 6·(-1) = -1 + 5 – 6 = -2 ⇒ B( -1 | -2 )
Dann brauchen wir „m“, und das bekommen wir über die Ableitung:
f'(x) = 3x2 + 10x + 6
⇒ mTan = f'(-1) = 3·(-1)2+10·(-1)+6 = -1
Wir kennen also x, y und m [x=-1, y=-2, m=-1] und können alles in y=m·x+b einsetzen:
yTan = m·x + b
⇒ -2 = -1·(-1) + b ⇒ -2 = 1 + b ⇒ b = -3 ⇒ yTan = -1·x–3
Um die Normalengleichung zu erhalten, berechnen wir zuerst die Normalensteigung und setzen dann wieder m und die Koordinaten von B in y = m·x+b ein.
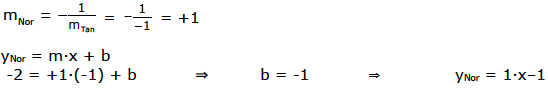
Beispiel b.
Sei f(x) = 0,5x2–2x+3
Bestimmen Sie die Gleichung der Tangente und der Normalen an f(x) im Punkt B(4|a) !
Lösung:
Wir berechnen zuerst die Koordinaten von B.
a=f(2) = 0,5·42 – 2·4 + 3 = 8 – 8 + 3 = 3 ⇒ B( 4 | 3 )
Nun brauchen wir „m“, das geht über die Ableitung:
f'(x) = 1x – 2
⇒ mTan = f'(4) = 1·4 – 2 = 2
Wir kennen x, y und m [x=4, y=3, m=2] und können alles in y=m·x+b einsetzen:
yTan = m·x + b
⇒ 3 = 2·4 + b ⇒ 3 = 8 + b ⇒ b = -5 ⇒ yTan = 2x–5
Um die Normalengleichung zu erhalten, berechnen wir wieder zuerst die Normalensteigung und setzen dann alles in y = m·x+b ein.
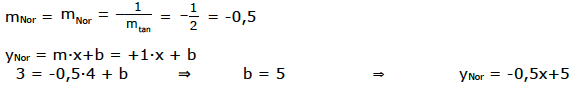
[A.15.02] Methode 2: Tangente und Normale berechnen über Tangentenformel und Normalenformel

Beispiel c.
Sei f(x) = x³+5x²+6x [gleiche Aufgabe wie oben Beispiel a.]
Bestimmen Sie die Gleichung der Tangente und der Normalen an f(x) im Punkt B(-1|f(-1)) !
Lösung:
Das Schöne an der Tangentenformel bzw. an der Normalenformel ist, dass man eigentlich nichts denken muss. Man berechnet f'(u) und f(u) und setzt einfach alles ein.
Zuerst berechnen wir noch die Ableitung.
f'(x) = 3x² + 10x + 6
u = -1
f(u) = f(-1) = (-1)3+5·(-1)2+6·(-1) = … = -2
f'(u) = f'(-1) = 3·(-1)2+10·(-1)+6 = -1
Nun setzen wir alles in die Formeln ein und sind fertig.
Berechnung der Tangente:
yTan = f'(u)·(x–u)+f(u) = f'(-1)·(x+1)+f(-1) =
= -1 · (x+1) + (-2) = -1x – 1 – 2 = -1x–3 ⇒ yTan = -1·x–3
Berechnung der Normale:
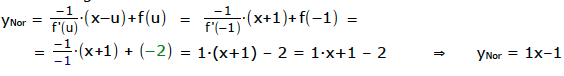
Beispiel d.
Sei f(x) = 0,5x²–2x+3 [gleiche Aufgabe wie oben Beispiel b.]
Bestimmen Sie die Gleichung der Tangente und der Normalen an f(x) im Punkt B(4|a) !
Lösung:
Zuerst beginnen mit der Berechnung der Ableitung.
f'(x) = 1·x – 2
u = 4
f(u) = f(4) = 0,5·42 – 2·4 + 3 = 8 – 8 + 3 = 3
f'(u) = f'(4) = 1·4 – 2 = 2
Nun setzen wir alles in die Formeln ein und sind fertig.
Berechnung der Tangente:
yTan = f'(u)·(x–u)+f(u) = f'(4)·(x–4)+f(4) =
= 2 · (x–4) + 3 = 2x – 8 + 3 = 2·x–5 ⇒ yTan = 2x–5
Berechnung der Normale:
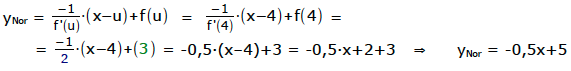
[A.15.03] Wendetangente bzw. Wendenormale
Eine Wendetangente bzw. eine Wendenormale ist nicht anderes, als eine Tangente bzw. eine Normale im Wendepunkt.
Der einzige Unterschied zu „normalen“ Tangentenaufgaben ist der, dass man zuerst den Wendepunkt berechnen muss.
Beispiel e.
Bestimmen Sie die Gleichung der Wendetangenten und der Wendenormale der Funktion ft(x) mit: 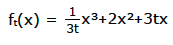
Lösung:
Da es sich um Wendetangente und Wendenormale handelt, wird der Berührpunkt logischerweise auch der Wendepunkt sein. Daher berechnen wir erstmal den Wendepunkt.

[A.15.04] Tangente von außen -- unbekannter Berührpunkt
Worum geht es überhaupt?
Gegeben sind eine Funktion f(x) und ein Punkt A, der nicht auf der Funktion liegt.
Gesucht sind eine [oder mehrere] Tangenten, die an der Funktion anliegen und durch den gegebenen Punkt A laufen.
Vorgehensweise:
Man verwendet die Tangentengleichung und setzt die Koordinaten des gegebenen Punktes A für x und y ein. [NICHT für „u“ einsetzen!! „u“ ist der x-Werts des Berührpunktes und den haben wir NICHT!]
Man erhält eine Gleichung mit „u“ als einziger Unbekannten.
Die Gleichung löst man von Hand oder mit dem GTR nach „u“ auf.
Beispiel f.
Bestimme die Gleichung der Tangenten an die Funktion: f(x) = x³–3x²+5x+4 , die durch den Punkt A( 1 | 9 ) geht.
Lösung:
f'(x) = 3x²–6x+5 [Ableitung ist immer gut]
Der Punkt A liegt nicht auf der Funktion f(x). [Setzt man den x-Wert von A in f(x) ein, kommt nicht 9 raus.]
Insbesondere gilt nicht mTan = f'(1).
Da wir den Berührpunkt nicht gegeben haben, schenken wir ihm großzügiger Weise die Koordinaten: B( u | f(u) )
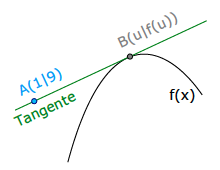
Ab nun stellen wir unsere Tangentengleichung auf:
yTan = f'(u) · (x–u) + f(u) ⇔ yTan =(3u²–6u+5)·(x–u) + u³–3u²+5u+4
Die Gleichung, die man hier links erhält, löst man normalerweise natürlich mit dem Taschenrechner. Hier möchten wir jedoch alles „von Hand“ rechnen.
Jetzt erst kommt unser Punkt A ins Spiel. A liegt zwar nicht auf der Funktion, aber dafür auf der Tangente. Also machen wir eine Punktprobe mit A.
A( 1 | 9 ) ⇒ xA=1, yA=9 einsetzen.

kurze Beispielaufgabe
Beispiel g.
Bestimmen Sie die Gleichung der Tangenten an f(x) = x3–3x2+4, die parallel zu y = 9x+16 sind !
Lösung:
Wenn die Tangenten parallel zu y =9x+16 sind, müssen auch sie die Steigung mTan = 9 haben.
⇒ 9 = mTan = f'(u)
9 = 3u2 – 6u |-9 |:3
u2 – 2u – 3 = 0
u1,2 = = 1± 2 ← a-b-c-Formel geht selbstverständlich ebenfalls
u1 = -1 u2 = 3
⇒ B1(-1|f(-1)) B2(3|f(3))
Jetzt können wir bereits die Tangentengleichungen berechnen:
[Ich kürze den Rest der Rechnung etwas ab. Ich verwende auch nur die Methode über die Tangentengleichung. Über y=m·x+b geht’s natürlich genau so gut]
erste Tangente: yTan = f'(-1)·(x–(-1))+f(-1) = 9·(x+1)+0 = 9x+9
zweite Tangente: yTan = f'(3)·(x–3) + f(3) = 9·(x–3) + 4 = 9x–25


