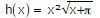Oberstufe
A.13.07 | vermischte Funktionstypen
In den bisherigen Kapiteln haben wir hauptsächlich Polynome („normale“ Funktionen) abgeleitet. Meistens müssen Sie jedoch Funktionen ableiten, in denen Sinus, Kosinus, e-Funktionen, Wurzeln, ln, etc.. vermischt werden. Das üben wir an dieser Stelle.
Es gibt themenverwandte Videos, die dir auch helfen könnten:
>>> [A.41.03] Ableitungen bei e-Funktionen (Basiswissen), [A.41.04] Ableitungen bei e-Funktionen (Herausforderung)
>>> [A.42.04] Ableitungen bei sin/cos-Funktionen (Basiswissen), [A.42.05] Ableitungen bei sin/cos-Funktionen (Herausforderung)
>>> [A.43.02] Ableitungen bei gebrochen-rationalen Funktionen (Basiswissen), [A.43.03] Ableitungen bei gebrochen-rationalen Funktionen (Herausforderung)
>>> [A.44.02] Ableitungen bei Logarithmus-Funktionen (Basiswissen), [A.44.03] Ableitungen bei Logarithmus-Funktionen (Herausforderung)
>>> [A.45.01] Ableitungen bei Wurzel-Funktionen (Basiswissen), [A.45.02] Ableitungen bei Wurzelfunktionen (Herausforderung)
Lerntipp:
Versuche die Beispiele zuerst selbstständig zu lösen, bevor du das Lösungsvideo anschaust.
Rechenbeispiel 1
Bestimmen Sie die Ableitung der folgenden Funktion: f(x) = x²+sin(2x)
Lösung dieser Aufgabe
Rechenbeispiel 2
Bestimmen Sie die Ableitung der folgenden Funktion: g(x) = x²·sin(2x)
Rechenbeispiel 3
Bestimmen Sie die Ableitung der folgenden Funktion: 
Rechenbeispiel 4
Bestimmen Sie die Ableitung der folgenden Funktion: f(x) = (2x+1)·e2–x
Rechenbeispiel 5
Bestimmen Sie die Ableitung der folgenden Funktion: 
Rechenbeispiel 6
Bestimmen Sie die Ableitung der folgenden Funktion: h(x) = 0,5·(e-2x–3)2
Rechenbeispiel 7
Bestimmen Sie die Ableitung der folgenden Funktion: f(x) = 2x²·ln(3x+1)
Rechenbeispiel 8
Bestimmen Sie die Ableitung der folgenden Funktion: g(x) = 2t²·ln(3x+1)
Rechenbeispiel 9
Bestimmen Sie die Ableitung der folgenden Funktion: 
