Studium
A.13.04 | Produktregel (Leibnizregel)
Die Produktregel oder auch Leibnizregel wendet man an, will man zwei Faktoren ableiten (die mit „Mal“ verbunden sind). In beiden Faktoren sollte die Variable („x“) auftauchen, anderenfalls muss man die Produktregel nicht zwingend anwenden. Hat die Funktion die Form: f(x)=u*v, so hat die Ableitung die Form: f'(x)=u'*v+u*v´.

 Es gibt themenverwandte Videos, die dir auch helfen könnten:
Es gibt themenverwandte Videos, die dir auch helfen könnten:


 Sobald du dieses Video verstehst, kannst du auch folgendes Thema angehen:
Sobald du dieses Video verstehst, kannst du auch folgendes Thema angehen:
>>> [A.13.06] Vermischte Aufgaben
>>> [A.13.07] vermischte Funktionstypen
Lerntipp:
Versuche die Beispiele zuerst selbstständig zu lösen, bevor du das Lösungsvideo anschaust.
Rechenbeispiel 1
Bestimmen Sie die Ableitung der Funktion über die Produktregel f(x) = x²·(x+5)
Rechenbeispiel 2
Bestimmen Sie die Ableitung der Funktion über die Produktregel 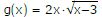
Rechenbeispiel 3
Bestimmen Sie die Ableitung der Funktion über die Produktregel h(x) = (3–x)2·(2x+4)3
Rechenbeispiel 4
Bestimmen Sie die Ableitung der Funktion über die Produktregel f(x) = (2x–1)·(x+3)2
Rechenbeispiel 5
Bestimmen Sie die Ableitung der Funktion über die Produktregel 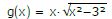
Rechenbeispiel 6
Bestimmen Sie die Ableitung der Funktion über die Produktregel h(x) = (2+x)4·(2x+4)3

