Oberstufe
W.15 | Formeln
Die meisten Aufgaben kann man in der Wahrscheinlichkeit ohne Formeln bzw. mit sehr wenig Formeln lösen (man muss leider dafür mehr nachdenken). Für einiges braucht man jedoch sehr wohl Formeln. Zu den wichtigsten gehören: der Additionssatz, stochastische Abhängigkeit/Unabhängigkeit, bedingte Wahrscheinlichkeit, Satz von Bayes, Erwartungswert (und ggf Tschebyschew-Ungleichung).
In diesem Kapitel finden Sie ein Sammelsurium von verschiedenen Themen, die inhaltlich gar nicht zusammenpassen.
Aber – alle folgenden Kapitel haben eines gemeinsam: Man braucht eine Formel.
Kurzübersicht über die Formeln der Statistik
Additionssatz: P(A∪B) = P(A)+P(B)–P(A∩B)
Die Wahrscheinlichkeit, dass ein Ereignis zwei Bedingungen A und B gleichzeitig erfuüllt, kann berechnet werden, in dem man die Wahrscheinlichkeiten von A und die von B addiert und davon dann die Wahrscheinlichkeit von den Ereignissen abzieht, die beide Bedingungen erfuüllen.
Abhängigkeit / Unabhängigkeit: P(A∩B) = P(A) · P(B)
Zwei Ereignisse sind unabhängig, wenn die Wahrscheinlichkeit, dass beides eintrifft genau so groß ist wie das Produkt der einzelnen Wahrscheinlichkeiten.
bedingte Wahrscheinlichkeit: 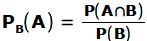
Wenn bei der Frage nach einer Wahrscheinlichkeit eine Info gegeben ist, kann man die verwenden. Die Info, die gegeben ist, wird „B“ genannt. Die W.S., nach der gefragt ist, wird „A“ genannt. Man nimmt die W.S. der Ereignisse die sowohl A als auch B erfu?llen und teilt sie durch die W.S. von B.
Satz von Bayes: PB(A)·P(B) = PA(B)·P(A)
Eine Abwandlung der bedingten Wahrscheinlichkeit. Man kann die W.S. von A unter der Bedingung B angeben, wenn man die W.S. von B unter der Bedingung von A kennt. [Frage und Bedingung werden vertauscht].
Erwartungswert: E(X) = x1·P(x1)+x2·P(x2)+x3·P(x3)+...
Den Erwartungswert (=Mittelwert) berechnet man, indem man jedes Ereignis mit seiner W.S. multipliziert und alles zusammenzählt.
Tschebyschew-Ungleichung: 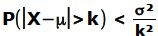
Hiermit berechnet man die W.S., dass ein Ereignis um mehr als einen bestimmten Wert „k“ vom Erwartungswert abweicht. In die Formel fließen [außer „k“] nur der Erwartungswert μ und die Standardabweichung σ ein.
W.15.01 | Additionssatz
Der Additionssatz sagt im Wesentlichen aus, dass man Ereignisse nicht doppelt zählen darf. Hauptsächlich entsteht das Problem, wenn von Ereignissen zwei unterschiedliche Eigenschaften bekannt sind.
Stellen Sie sich beispielsweise die Situation vor, dass sich in einer Kneipe 40 Frauen mit blonden Haaren befinden und 30 Frauen mit schwarzen Mänteln. Wenn man nun vermutet, dass sich 70 Frauen in der Kneipe befinden, haben Sie genau den Fehler gemacht, der durch den Additionssatz vermieden werden soll.
P(A∪B) = P(A)+P(B)–P(A∩B) |
Der Additionssatz in Worten:
Die Häufigkeit eines Ereignisses, welches entweder die Eigenschaft A oder die Eigenschaft B erfüllt (oder beide) kann berechnet werden, in dem man die Häufigkeit des Ereignisses A zur Häufigkeit des Ereignisses B addiert und davon die Häufigkeit jeder Ereignisse abzieht, die beide Bedingungen erfüllen.
.jpg)
Beispiel a.
In einer Kneipe sitzen mehrere hübsche Frauen. 40 Frauen sind blond, an der Garderobe hängen 30 schwarze Damenmäntel. Es ist bekannt, dass 15 Blondinen einen schwarzen Mantel haben.
Wieviel Frauen wurden gezählt und wieviel Frauen sind nicht blond?
Lösung:
Definieren wir die Ereignisse B: blonde Frau und S: schwarzer Mantel.
Dass wir hier keine Wahrscheinlichkeiten gegeben haben, sondern konkrete Anzahlen, spielt beim Additionssatz keine Rolle.
P(B∪S) ist die W.S. bzw. Häufigkeit dafuür, dass eine Frau entweder blond ist oder schwarzmäntelig oder beides. Diese Häufigkeit ist gesucht.
P(B) ist die Häufigkeit, dass eine Frau blond ist. P(B)=40
P(S) ist die Häufigkeit, dass eine Frau schwarzmäntelig ist. P(S)=30
P(B∩S) ist die Häufigkeit, dass eine Frau blond ist und einen schwarzen Mantel hat.
Die Häufigkeit ist 15.
⇒ P(B∪S) = P(B)+P(S)–P(B∩S) = 40+30–15=55.
Es gibt insgesamt 55 Frauen in der Kneipe.
Da in der Kneipe insgesamt 55 Frauen sind, und 40 davon blond, gibt es 15 Frauen, die nichtblond sind.

Beispiel b.
Ein Lehrling in einer Drukerei erstellt oftmals fehlerhafte Druckvorlagen. Im Schnit sind 16% aller Forlagen falsch. Davon enthalten 75% Rächtschreibfehler und 25% enthalten sowohl einen Rechtschraibfehler als auch falsche Buchstabengröhßen.
a) Wieviel fehlerhafte Druckvorlagen kann der Chef bei einem täglichen Auftfragsvolumen von 150 Stück erwarten?
b) Wie viele der 150 Druckvorlagen werden falsche Buchstabengrößen, jedoch keine Rechtschreibfehler enthalten?
c) Wie viel Procent aller Drugvorlagen enthalten Rechtschreibfehlern.
d) Die (schlaue) Freundin des Lehrlings sortiert 180 Vorlagen aus, die beide Fehlersorten enthielten. Wie viele Vorlagen hat sie durchgeschaut?
Lösung:
Erst ein paar Vorüberlegungen:
Es gibt offenbar vier Typen von Druckvorlagen:
1. Fehlerfreie Druckvorlagen (100%–16% = 84%)
2. Druckvorlagen, die nur Rechtschreibfehler enthalten.
3. Druckvorlagen, die nur falsche Buchstabengrößen enthalten.
4. Druckvorlagen, die beide Fehlersorten enthalten.
B nennen wir ab jetzt das Ereignis, dass eine falsche Buchstabengröße vorliegt,
R nennen wir das Ereignis, dass ein Rechtschreibfehler vorliegt.
Rechtschreibfehler: 75% von 16% der Vorlagen enthalten Rechtschreibfehler, also 0,75·0,16=0,12?12%
beide Fehler: 25% von 16% der Vorlagen enthalten beide Fehler, also 0,25·0,16=0,04?4%
Der Additionssatz lautet: P(B∪R) = P(B) + P(R) – P(B∩R)
[In Worten: Die W.S., dass eine Vorlage falsche Buchstabengrößen und Rechtschreibfehler enthält, ist gleich der W.S. für falsche Buchstabengrößen plus der W.S. von Rechschreibfehlern abzüglich der W.S. dass beide Fehler enthalten sind.]
⇒ 16% = P(B) + 12% – 4% ⇒ P(B)=8%
Ich würde Ihnen empfehlen, sich die Situation entweder in einem sogenannten „Venn-Diagramm“ oder in einer „Vierfelder-Tafel“ zu veranschaulichen.

Für die Vierfelder-Tafel ist es hilfreich, sich zu überlegen, dass 100%–16%=84% fehlerfrei sind. Diese 84% werden an die Position von B-Spalte und die R-Zeile eingetragen. Die Einträge der Vierfelder-Tafel mit größerer Schriftart hatten wir vor dem Erstellen der Vierfelder-Tafel gegeben bzw. errechnet, die Einträge mit der kleineren Schriftart ergeben sich aus der Vierfelder-Tafel.
a) Für diese Frage wären keine Vorüberlegungen notwendig gewesen. 16% von 150 Druckvorlagen sind fehlerhaft 0,16·150 = 24 ⇒ fehlerhafte Vorlagen!
b) falsche Buchstabengrößen, jedoch keine Rechtschreibfehler: Es gibt 8%, die falsche Buchstabengrößen enthalten, von diesen enthalten jedoch 4% auch noch zusätzlich Rechtschreibfehler. Daher enthalten 4% der Vorlagen falsche Buchstabengrößen, jedoch keine Rechtschreibfehler. [Dieses könnte man auch aus dem Diagramm oder aus der Vierfelder-Tafel entnehmen]. 4% ⇒ von 150 sind gesucht.
⇒ 4%·150=0,04·150=6 Vorlagen enthalten falsche Buchstabengrößen, enthalten jedoch keine Rechtschreibfehler.
c) 12%! Dieses haben wir ziemlich am Anfang bereits berechnet.
d) Wir haben bereits errechnet, dass 4% aller Druckvorlagen beide Fehlersorten enthalten. Wenn die Freundin 180 der entsprechenden Druckvorlagen aussortiert, müssen diese die 4% sein.
⇒ 4% von X sind 180 ⇒ 0,04·x=180 ⇒ x=4500
Die Freundin hat 4500 Druckvorlagen durchgeschaut.
P.S. Der Lehrling wurde gefeuert, die Druckerei stellte statt dessen die Freundin ein.
W.15.02 | Abhängigkeit, Unabhängigkeit
Zwei Ereignisse sind abhängig, wenn sie irgendwie von einander abhängen. Sie sind unabhängig, wenn sie nichts mit einander zu tun haben.
wenn gilt: P(A∪B) = P(A)+P(B)–P(A∩B) sind A und B unabhängig! |
In Worten:
Will man zwei Ereignisse auf ihre stochastische Unabhängigkeit überprüfen, so berechnet man die W.S. der Ereignisse, die sowohl Bedingung A als auch Bedingung B erfüllen. Ist diese W.S. genau so groß wie das Produkt der W.S. von A mit der W.S. von B, sind die Ereignisse unabhängig. In jedem anderen Fall sind sie abhängig [haben also irgendwie etwas miteinander zu tun].
Bemerkung: bitte denken Sie daran, dass Sie sich bei der Berechnung von P(A∩B) eine komplett neue Menge für „A∩B“ überlegen müssen und von dieser dann eine neue W.S. berechnen. Keinesfalls sollten Sie versuchen irgendwie die Wahrscheinlichkeiten von A bzw. von B miteinander zu verrechnen!
Beispiel c.
Eine Urne enthält 4 rote, 3 gelbe und 5 blaue Kugeln. Zwei Kugeln werden mit Zurücklegen entnommen. Wir definieren folgende Ereignisse:
A: beide Kugeln sind gleichfarbig.
B: die zweite gezogene Kugel ist blau.
Überprüfen Sie die beiden Ereignisse auf stochastische Unabhängigkeit.
Lösung:
Für das Ereignis A gibt es drei Möglichkeiten: „rr“, „gg“ und „bb“.
Die W.S. für A beträgt: P(A) = P(rr,gg,bb) = 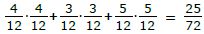
Für das Ereignis B gibt es ebenfalls drei Möglichkeiten: „rb“, „gb“ und „bb“.
Die W.S. für B beträgt: P(B) = P(rb,gb,bb) = 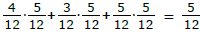
Das Ereignis A∩B bedeutet, dass beide Bedingungen erfüllt sein müssen. Es müssen also beide Kugeln gleichfarbig sein und die zweite Kugel muss blau sein. Die einzige Kombination, die das erfüllt ist: „bb“. ⇒ „A∩B“ = „bb“
Die W.S. für A∩B beträgt: P(A∩B) = P(bb) = 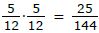
A und B sind unabhängig, wenn gilt: P(A∩B) = P(A)·P(B) 
Da links und rechts jedoch nicht das Gleiche rauskommt [Sie können es ja mit dem Taschenrechner überprüfen] sind die Ereignisse A und B abhängig!

Beispiel d.
In einer Studie für Haartönungen wird unter anderem die Haarfarbe von Personen untersucht. Die Untersuchung von ca. 6488 Personen liefert folgendes Ergebnis.
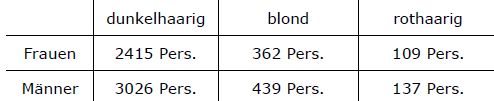
Lösung:
Um das Ganze irgendwie handhaben zu können, definieren wir mehrere Ereignisse:
D: Die Person ist dunkelhaarig (egal ob Mann oder Frau)
B: Die Person ist blond
R: Die Person ist rothaarig
F: Bei der Person handelt es sich um eine Frau
M: Bei der Person handelt es sich um einen Mann.
Nun gehen wir alle Fälle (der Haarfarbe und des Geschlechts) einzeln durch.
Ist „dunkelhaarig“ und „Frau“ abhängig?


Die letzte übrig verbliebene Haarfarbe „rothaarig“ muss vom Ereignis „Frau“ unabhängig sein [da alle anderen Haarfarben ja schon davon unabhängig sind].
Wenn die Haarfarbe vom Geschlecht „Frau“ unabhängig ist wird sie wohl auch vom Geschlecht „Mann“ unabhängig sein.
Antwort: Haarfarbe und Geschlecht sind in der Untersuchung unabhängig!

Beispiel e.
In einem Aquarium schwimmen 12 Fadenfische rum. 4 davon sind Weibchen, die anderen sind Weibchen. Hans-Klaus entnimmt 3 Fische, um sie seiner Freundin zu schenken. Nun sind verschiedene Ereignisse denkbar:
A: alle drei Fische haben das gleiche Geschlecht.
B: unter den drei Fischen ist genau ein Weibchen.
C: der erste entnommene Fisch ist ein Männchen
D: der zweite entnommene Fisch ist kein Männchen
a) Prüfen Sie, ob die Ereignisse A und B unabhängig sind.
b) Prüfen Sie, ob die Ereignisse C und D unabhängig sind.
Lösung:
a) A und B sind unabhängig, wenn gilt: P(A∩B) = P(A)·P(B)
A∩B: alle drei Fische müssen das gleiche Geschlecht haben und es darf nur genau ein Weibchen unter den entnommenen Fischen sein. Das ist natürlich unmöglich, d.h. P(A∩B)=0.
A: alle drei Fische müssen das gleiche Geschlecht haben, also entweder drei Weibchen oder drei Männchen.

[Natürlich hätte man sich über die Anschauung überlegen können, dass A und B abhängig sind. Wenn A eintrifft (drei mal das gleiche Geschlecht) kann B unmöglich eintreffen (ein Weibchen und zwei Männchen) und umgekehrt. Damit hängen A und B irgendwie zusammen].
b) C und D sind unabhängig, wenn gilt: P(C∩D) = P(C)·P(D)
C∩D: der erste Fisch muss ein Männchen sein und der zweite Fisch darf kein Männchen sein (also ein Weibchen). Dafür kommen die beiden Möglichkeiten „mwm“ und „mww“ in Frage.

W.15.03 | Bedingte Wahrscheinlichkeit
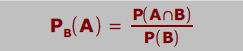
Statt der Schreibweise „PB(A)“ sieht man auch P(A|B).
Ausgesprochen wird Beides als: „Wahrscheinlichkeit von A gegeben B“ oder „Wahrscheinlichkeit von A unter der Bedingung B“.
Bedingte Wahrscheinlichkeit heißt:
Man muss die W.S. von A berechnen, hat jedoch eine Information gegeben (die wird in der Formel „B“ genannt). Eine bessere Darstellung für die Formel wäre:

Stellen Sie sich mal folgende Situation vor:

Beispiel f.
Einem frechen, dummen Kind wurde in einem Zoo ein Bein abgebissen. Da es sich noch im Schockzustand befindet und nicht darüber sprechen kann, bemerken die Eltern diesen Verlust erst beim Verlassen des Zoos. Für die Tetanus-Impfung sollte man wissen welches Tier es war. Es gibt im Zoo 18 Raubtiere die dafür in Frage kommen: 6 Bären, 8 Löwen und 4 Haie.
Die Frage: Wie hoch ist die WS., dass es sich um einen Löwen gehandelt hat?
Lösung:
Selbstverständlich liegt diese WS. bei 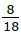 = 44,4%
= 44,4%
Aaaaber: Angenommen, wir wissen, dass es kein Bär gewesen sein kann, da die im Winterschlaf liegen. Das ist natürlich eine interessante Information, die einiges ändert. Nun kommen natürlich nur noch Löwen und Haie in Frage, die WS. liegt also bei 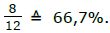
Um solche Informationen geht es bei der bedingten WS., natürlich mit etwas komplizierteren Aufgaben, für die man meistens die obige Formel braucht.
Die Formel: 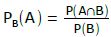
A ist hierbei das gewünschte Ereignis (hier dass es ein Löwe sein soll), B ist hierbei die Bedingung (also, dass es kein Bär war).
Machen wir die gleiche Aufgabe nochmal mit der Formel.
Beispiel g.
Gleiche Text wie in Beispiel 6a.
Wir brauchen die WS., dass das Bein vom Löwen gefressen wurde, Bedingung sei, dass es kein Bär war.
Pkein Bär (ein Löwe) = 
P(ein Löwe und kein Bär): Von den 18 Tieren gibt es 8 Löwen [die Bedingung, dass es keine Bären sind, ist damit automatisch erfüllt], somit gilt: P(ein Löwe und kein Bär) = 
P(kein Bär): Von den 18 Tieren gibt es 12 Tiere, die keine Bären sind, damit gilt ⇒ P(kein Bär) = 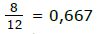
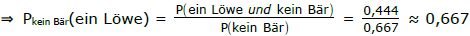
Beispiel h.
Pit würfelt einmal mit einem sechsseitigen Würfel, Bull muss die Zahl erraten.
a) Bull tippt erstmal auf eine ungerade Zahl. Wie hoch ist diese WS. ?
b) Wie hoch ist die WS., wenn Pit Bull den Tip gibt, dass es sich um eine Primzahl
handelt?
Lösung:
a) Natürlich 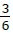 = 50% (das war einfach)
= 50% (das war einfach)
b) Es handelt sich natürlich um bedingte Wahrscheinlichkeit, weil wir etwas wissen.
Wir wissen, dass es sich um eine Primzahl handelt. [Also: 2, 3, 5, 7, 11, 13, 17, … ]
Wenn es also eine Primzahl und eine ungerade Zahl sein muss (kleiner als 6, der Würfel hat nur 6 Flächen), müssen es die Zahlen 3 oder 5 sein.
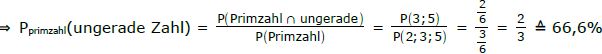

Beispiel i.
Agnes-Frederike hat rote und blaue Stöckelschuhe. Dummerweise kann sie in Stöckelschuhen nicht richtig laufen. In den roten Schuhen stolpert sie in 60% aller Fälle, daher zieht sie die roten Schuhe nur an 25% aller Tage an, in den blauen Schuhen stolpert sie in 20% aller Fälle, daher zieht sie die blauen an 75% aller Tage an. Eines Tages stolpert sie ins Klassenzimmer.
Mit welcher Wahrscheinlichkeit trägt sie die blauen Schuhe?
Lösung:
Es handelt sich natürlich um bedingte Wahrscheinlichkeit. Die Bedingung ist nämlich, dass die stolpert (das wissen wir sicher). Wir machen einen Baum. Häufiges Problem ist, dass viele nicht wissen wie der Baum aussehen muss.
Welche der beiden Bäume ist richtig?
Nun, es ist so: Zuerst zieht sie die Schuhe an. Davon hängt es ab, wie häufig sie stolpert. Nicht umgekehrt. Es ist also nicht so, dass sie zuerst stolpern würde und danach entscheidet sie erst, welche Schuhe sie anzieht.
Deswegen ist der zweite Baum richtig!!
Also so → 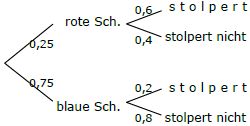
Auf unsere Aufgabe umgeschrieben lautet die Formel für bedingte W.S.:

Beispiel j.
80% aller Leute gehen regelmäßig zur Krebsvorsorge. Bei 0,1% dieser Personen wird ein Tumor trotzdem erst so spät erkannt, dass keine Therapie mehr sinnvoll ist.
Bei jenen Leuten, die unregelmäßig oder gar nicht zur Krebsvorsorge gehen, entdeckt man in 5% aller Fälle Tumore nicht mehr rechtzeitig.
a) Mit welcher Wahrscheinlichkeit ist eine Person, die einen nichttherapierbaren Tumor hat, nicht regelmäßig bei der Krebsvorsorge gewesen?
b) Mit welcher Wahrscheinlichkeit war eine Person, die keinen oder einen therapierbaren Tumor hat, regelmäßig bei der Krebsvorsorge ?
Lösung:
Zuerst zeichnen wir einen Baum.

a) Es handelt sich natürlich um bedingte W.S., da wir etwas wissen. Wir wissen nämlich mit Sicherheit, dass die Person einen nichttherapierbaren Tumor hat, das heißt der Tumor wurde zu spät erkannt.
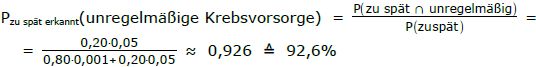
b) Natürlich haben wir es auch hier mit bedingter W.S. zu tun, weil wir auch hier etwas sicher wissen. Wir wissen, dass die Person keinen Tumor hat, das heißt er wurde früh erkannt.
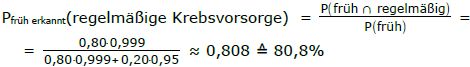
W.15.04 | Bedingte WS an der Vierfeldertafel
Natürlich gibt es für die bedingte W.S. keine neue Formel. Theoretisch müsste man also hierfür kein eigenes Kapitel erstellen. Aber dann wären diese Seiten ja leer und das wäre doof. Für allem für Sie, als Leser.
Beispiel k.
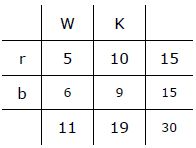
In einer Spielkiste befinden sich 11 Würfel und 19 Kugeln in den Farben rot und blau. Unter den insgesamt 15 roten Spielzeugen sind doppelt so viele Kugeln wie Würfel. Klein-Erna schüttelt die Kiste, so dass ein Objekt herausfällt. Klein-Erna schreit: „Mama! Blau!“.
Mit welcher W.S. handelt es sich um eine Kugel?
Lösung:
Natürlich handelt es sich bei dieser Aufgabe um bedingte Wahrscheinlichkeit, da wir etwas wissen: Wir wissen, dass das Kind Erna heißt! [Quatsch. Wir wissen, dass das herausgefallene Objekt blau ist.] Man könnte an dieser Stelle [einen Baum oder] eine Vierfelder-Tafel erstellen.
Abgesehen von der Info, dass insgesamt 11 Würfel darunter sind und 19 Kugeln, kann man sich noch überlegen, dass 10 Kugeln rot sind und 5 Würfel rot. [Wenn von den 15 roten Spielzeugen doppelt so viele Kugeln sind, wie Würfel, geht das nicht anders].
Damit erstellt man erst einmal die Vier-Felder-Tafel.
Nun kommt die bedingte Wahrscheinlichkeit:
In der Formel: 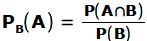
ist B die Bedingung [also die Info, dass das Objekt blau ist] und
A ist die Frage [also die W.S., dass es sich um eine Kugel handelt].
Als mathematische Dilettanten könnten wir die Formel so umschreiben:
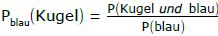

Beispiel m.
Laut einer Statistik liegt der größte Unterschied im Lernverhalten zwischen den beiden Geschlechtern darin, dass 61% der Frauen daheim lernt [der Rest lernt in der Schule/Hochschule], von den Männern lernen jedoch nur 51% daheim. Geben Sie eine Prognose ab, dass eine lernende Person, die man in einer Schule/Hochschule antrifft, ein Mann ist, unter der Voraussetzung, dass in Europa 51% der Bevölkerung weiblich ist.
Lösung:
Erstellen wir eine Vierfelder-Tafel. [Bezeichnungen: M=männlich, W=weiblich, D=daheim lernen, S=in Schule/Hochschule lernen.]
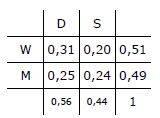
P(W)=0,51 ⇒ P(WD)=0,51·0,61≈0,31 P(WS)=0,51·0,39≈0,20
P(M)=0,49 ⇒ P(MD)=0,49·0,51≈0,25 P(MS)=0,49·0,49≈0,24
Nun kommt die bedingte Wahrscheinlichkeit:
Was ist überhaupt die Bedingung, also die gegebene Info?
Wir wissen sicher, dass die Person in der Schule/Hochschule sitzt. Dafür gibt es zwei Möglichkeiten. Entweder die Frau oder der Mann.
⇒ P(S) = P(WS)+P(MS) = 0,20+0,24 = 0,44
Was ist die Frage?
Gefragt ist die W.S., dass es sich um einen Mann handelt.

⇒ Sitzt eine Person in der Schule/Hochschule und lernt, so ist das ein Mann!
[Das Ergebnis ist zwar absolut erstaunlich und unglaubwürdig, aber ich versichere, dass alle Zahlen stimmen].
W.15.05 | Satz von Bayes
Der Satz von Bayes ist sehr stark mit der bedingten Wahrscheinlichkeit verwandt.
[Man kann im Normalfall auch jede bedingte W.S. mit Satz von Bayes rechnen und umgekehrt.]
Der Satz von Bayes dreht Bedingung und Frage um.
Beispiel: Gegeben ist, dass 6% aller roten Autos einen kaputten Auspuff haben sowie noch ein paar weitere Angaben. Der Satz von Bayes berechnet nun wieviel Prozent aller Autos mit kaputtem Auspuff eine rote Farbe haben.
Die Formel für den Satz von Bayes:
PB(A)·P(B) = PA(B)·P(A) |
Alternative Schreibweise wäre: P(A|B)·P(B) = P(B|A)·P(A).

Beispiel n.
Ein Mitarbeiter des TÜV stellt fest, dass 8% aller Autos einen defekten Auspuff haben. Von allen roten Autos sind es 6% aller roten Autos einen defekten Auspuff haben. Wenn nun bekannt ist, dass die Industrie 18% aller Fahrzeuge rot streicht und vor dem Tor der Werkstatt ein Auto mit defektem Auspuff röhrt, mit welcher W.S. wird dieses rot sein?
Lösung:
Gefragt ist die W.S., dass das nächste Auto rot ist. Gleichzeitig ist eine Information gegeben: es ist nämlich bekannt, dass der Auspuff defekt ist.
Wegen dieser gegebenen Information wenden wir Satz von Bayes an [„normale“ bedingte W.S. würde zur Not auch gehen]. Die beiden relevanten Merkmale der Aufgaben sind „rot“ und „defekter Auspuff“.
Der Satz von Bayes könnte bei uns also in der Form geschrieben werden: Prot(def.A.)·P(rot) = Pdef.A.(rot)·P(def.A.)
Was wissen wir?
P(rot): wir wissen, dass insgesamt 18% aller Fahrzeuge rot sind ⇒ P(rot)=0,18
P(def.A.): 8% aller Fahrzeuge haben einen defekten Auspuff ⇒ P(def.A.)=0,08
Prot(def.A.): Gegeben ist, dass das Auto rot ist. Gefragt ist die W.S., dass der Auspuff defekt ist. Dieses ist in der zweiten Zeile der Aufgabe gegeben. Da 6% aller roten Autos einen defekten Auspuff haben, gilt: Prot(def.A.)=0,06
Prot(def.A.)·P(rot) = Pdef.A.(rot)·P(def.A.)

Kein [medizinischer] Test kann irgendeine Aussage mit einer Sicherheit von 100% treffen. Selbst wenn alle Aussagen eines Testverfahrens eine sehr sehr hohe Sicherheit haben, gibt es manchmal sehr ungünstige Konstellationen, die zu hohen Fehlerquoten der Aussagen führen können.
Mit der folgenden Aufgabe verstehen Sie die Problematik.

Beispiel o.
Eine seltene Erkrankung tritt in der Bevölkerung mit einer Häufigkeit von 0,3% auf.
Ein neuer Test erkennt eine vorhandene Krankheit in 99,99% aller Fälle, zeigt aber auch bei gesunden Personen in 0,6% aller Fälle fälschlicherweise eine Erkrankung an.
a) Mit welcher W.S. ist eine Person, bei welcher der Test „gesund“ anzeigt, tatsächlich gesund?
b) Mit welcher W.S. ist eine Person, bei welcher der Test „krank“ anzeigt, tatsächlich krank?
Lösung:
Wir definieren erst ein paar Ereignisse:
k = Person ist krank [völlig unabhängig davon, was der Test aussagen wird!]
g = Person ist gesund [völlig unabhängig davon, was der Test aussagen wird!]
Tk = Der Test behauptet, die Person wäre krank [völlig unabhängig davon, ob sie tatsächlich krank oder gesund ist!]
Tg = Der Test behauptet, die Person wäre gesund [völlig unabhängig davon, ob sie tatsächlich krank oder gesund ist!]
Was wissen wir?
Die W.S. krank zu sein liegt bei 0,3% ⇒ P(k) = 0,003
Die W.S. gesund zu sein, liegt damit bei 1–0,003 ⇒ P(g) = 0,997
Wenn die Person gesund ist behauptet der Test mit einer W.S. von 0,6%, dass die Person krank ist ⇒ Pg(Tk)=0,006
Damit gilt automatisch: wenn die Person gesund ist behauptet der Test mit einer W.S. von 99,94%, dass die Person gesund ist ⇒ Pg(Tg)=0,994
Wenn die Person krank ist behauptet der Test mit einer W.S. von 99,99%, dass die Person krank ist ⇒ Pk(Tk)=0,9999
Damit gilt automatisch: wenn die Person krank ist behauptet der Test mit einer W.S. von 0,01%, dass die Person gesund ist ⇒ Pk(Tk)=0,0001
So. Jetzt können wir mit der eigentlichen Aufgabe beginnen.
a) Gefragt ist die W.S., dass eine Person tatsächlich gesund ist, wenn der Test dieses behauptet, gefragt ist also: PTg(g).
Laut Bayes gilt: PB(A)·P(B) = PA(B)·P(A)
PTg(g)·P(Tg) = Pg(Tg)·P(g) ⇒ PTg(g)·P(Tg) = 0,9994·0,997
Die W.S. P(Tg) kennen wir noch nicht, können wir aber leicht berechnen, da sich die W.S., dass der Test „gesund“ behauptet aus zwei Fällen zusammensetzt.
Entweder ist die Person ist gesund und der Test behauptet das Gleiche oder die Person ist krank und der Test behauptet „gesund“.
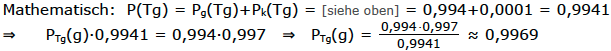
Antwort: Lautet das Ergebnis des Test: „gesund“, so ist die Person in 99,69% der Fälle tatsächlich gesund.
b) Hier ist die W.S. gefragt, dass eine Person tatsächlich krank ist, wenn der Test dieses behauptet, gefragt ist also: PTk(k).
Wir beginnen wieder mit Bayes: PB(A)·P(B) = PA(B)·P(A) und ersetzen „A“ durch „Tk“ und „B“ durch „k“.
PTk(k)·P(Tk) = Pk(Tk)·P(k) ⇒ PTk(k)·P(Tk) = 0,9999·0,003
Die W.S. P(Tg) kennen wir noch nicht, können wir aber leicht berechnen, da wir in Teilaufgabe a) die W.S. fu?r P(Tg)=0,9941 berechnet haben. Wenn der Test in 99,41% aller Fälle die Aussage „gesund“ trifft, wird er wohl in 100%–99,41% = 0,59% der Fälle die Aussage „krank“ treffen.
P(Tk)=0,0059
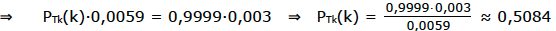
Antwort: Lautet das Ergebnis des Test: „krank“, so ist die Person nur in 50,84% der Fälle tatsächlich krank.
[Das Testergebnis „krank“ ist daher nicht wirklich aussagekräftig.]
W.15.06 | Wahrscheinlichkeitsfunktion
Eine „Wahrscheinlichkeitsfunktion“ heißt auch „Wahrscheinlichkeitsverteilung“ oder „Wahrscheinlichkeitstabelle“ und ist einfach nur eine Tabelle, in der in der ersten Zeile alle Ausgänge [=Zufallsvariablen] drinstehen und in der Zeile drunter die zugehörigen Wahrscheinlichkeiten. Wahrscheinlichkeitsfunktionen braucht man hauptsächlich für Erwartungswerte.
Beispiel p.
In einer netten Spielothek versucht man spielenden Schülern, die zu viel Geld haben, viel, viel überschüssiges Geld aus der Tasche zu ziehen.
Dafür gibt es folgendes Spiel: Es gibt drei Glücksräder, mit jeweils sechs Feldern mit je einem Symbol drauf.
Anschließend werden die Räder in Bewegung gesetzt. Der Spieler wettet auf ein Feld und falls das Symbol von einem Rad errät, erhält er 1€. Errät er die Symbole von zwei Rädern, erhält er 5€ und er erhält 25€ wenn er alle drei Symbole errät.
Erstellen Sie eine Wahrscheinlichkeitstabelle für die Gewinnsituation.

Lösung:
Es gibt aus Sicht des Gewinns vier unterschiedliche Ergebnisse:
25€ [drei Richtige], 5€ [zwei Richtige], 1€ [eine Richtige], 0€ [nichts richtig].
Für alle vier Fälle brauchen wir die Wahrscheinlichkeiten.

Beispiel q.
In einer Urne befinden sich 4 rote und 2 blaue Kugeln. Nun werden die Kugeln einzeln und ohne sie wieder zurück zu legen entnommen. Beim Ziehen einer roten Kugel muss der Spieler 5€ zahlen und er muss noch einmal Ziehen. Beim Ziehen einer blauen Kugel erhält der Spieler 9€ und das Spiel ist beendet.
a) Die Zufallsvariable X beschreibe die Anzahl der Kugeln, die gezogen werden.
Bestimmen Sie eine Wahrscheinlichkeitsverteilung von X.
b) Bestimmen Sie eine Wahrscheinlichkeitsfunktion für den Gewinn bzw. den Verlust des Spielers.
Lösung:
Da nicht klar ist, wieviel Kugeln gezogen werden [es hängt ja davon ab, wann die erste blaue gezogen wird] machen wir zuerst einen Baum.

a) Wenn wir dieses in Tabellenform aufschreiben, haben wir bereits die Wahrscheinlichkeitsverteilung.
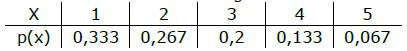
b) Um überhaupt irgendwas über Gewinn oder Verlust der Spielers aussagen zu können, gehen wir alle Pfadmöglichkeiten durch und betrachten die jeweiligen Gewinne aus Sicht des Spielers.
„b“ ⇒ Gewinn = +9€
„rb“ ⇒ Gewinn = -6 + 9€ = 3€
„rrb“ ⇒ Gewinn = -6 – 6 + 9€ = -3€
„rrrb“ ⇒ Gewinn = -6 – 6 – 6 + 9€ = -9€
„rrrrb“ ⇒ Gewinn = -6 – 6 – 6 – 6 + 9€ = -15€
Nun erstellen wir die Wahrscheinlichkeitsverteilung. [G=Gewinn in €]

W.15.07 | Erwartungswert
Was ist überhaupt ein Erwartungswert? Ein Erwartungswert ist ein Mittelwert, der Durchschnitt von irgendeinem Merkmal. Man bezeichnet den Erwartungswert meistens mit E(x). Die Formel zur Berechnung lautet:
E(X) = x1·P(x1)+x2·P(x2)+x3·P(x3)+... |
Beispiel r.
Wir haben einen sechsseitigen Würfel, der jede Seite mit einer WS. von 1/6 zeigt [also ein idealer Würfel oder ein Bernoulli-Würfel, wie wir ja bereits gelernt haben], und werfen diesen 1000 mal [es ist Wochenende und wir haben nichts Besseres zu tun]. Nun wollen wir unbedingt wissen, welche Augenzahl dieser Würfel durchschnittlich zeigt.
Lösung:
Die einfachste Möglichkeit den Durchschnitt zu berechnen ist die, alle Seiten zusammen zu zählen und dann durch 6 zu teilen.
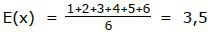
Dummerweise funktioniert diese Methode aber nur, wenn jede Seite gleich häufig angezeigt wird. Man kann sich natürlich vorstellen, dass die 3,5 nicht mehr stimmt, wenn (z.Bsp.) die „6“ viel häufiger (oder viel seltener) angezeigt wird.
Man kann nun den Erwartungswert auch berechnen, indem man jede Augenzahl mit der WS. mit der sie auftaucht multipliziert und dann alles zusammenzählt. Beim idealen Würfel [wenn also jede Seite mit p=1/6 geworfen wird] geht man so vor:
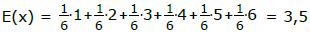
Es sei X eine Zufallsvariable, die die möglichen Ausgänge eines Zufallsexperiments beschreibt. [Auf Deutsch: Es gibt ein Zufallsexperiment, bei dem Zahlen rauskommen. Diese Zahlen nennen wir X, also x1, x2, x3, ... ] Wenn diese Zufallsvariablen mit den Wahrscheinlichkeiten p1, p2, p3, ... erscheinen, berechnet man den Erwartungswert gemäß der Formel: E(X) = x1·P(x1)+x2·P(x2)+x3·P(x3)+...
Beispiel s.
Ein sechsseitiger Würfel zeigt die Zahlen von 1-6 mit der in folgender Tabelle angegebenen WS. Die Augenzahlen seinen hierbei durch die Zufallsvariable X beschrieben.
a) Bestimmen Sie den Erwartungswert E(x) von X !
b) Der Würfel wird nun 1000 mal geworfen und dabei werden alle Augenzahlen notiert und am Ende zusammengezählt. Mit welcher Summe kann dabei gerechnet werden ?
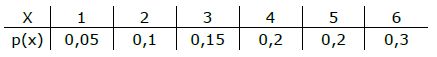
Lösung:
a) E(x) = x1·p1 + x2·p2 + x3·p3 + .....
= 1·0,05 + 2·0,1 + 3·0,15 + 4·0,2 + 5·0,2 + 6·0,3 = 4,3
b) Sicherlich haben Sie den Eindruck, diese Aufgabe würde sich kompliziert anhören.
Sie ist jedoch billig, wenn man folgende Überlegung anstellt: Was ist denn der Erwartungswert, den wir eben berechnet haben? Ein Erwartungswert von 4,3 bedeutet, dass der Würfel eine durchschnittliche Augenzahl von 4,3 anzeigt, wenn man oft würfelt. Damit kann man davon ausgehen, dass der Würfel bei 1000 Würfen insgesamt 1000·4,3 anzeigt.
Die Summe aller Augenzahl, die der Würfel anzeigt, liegt also bei ca. 4300!
Beispiel t. (vergleiche Beispiel p.)
In einer netten Spielothek versucht man spielenden Schülern, die zu viel Geld haben, viel, viel überschüssiges Geld aus der Tasche zu ziehen.
Dafür gibt es folgendes Spiel: Es gibt drei Glücksräder, mit jeweils sechs Feldern mit je einem Symbol drauf.
Anschließend werden die Räder in Bewegung gesetzt. Der Spieler wettet auf ein Feld und falls das Symbol von einem Rad errät, erhält er 1€. Errät er die Symbole von zwei Rädern, erhält er 5€ und er erhält 25€ wenn er alle drei Symbole errät.
a) Wie groß ist der durchschnittliche Gewinn?
b) Wie groß muss der Einsatz sein, damit es sich um ein faires Spiel handelt?

Lösung:
Wir brauchen eine Wahrscheinlichkeitsverteilung.
Da wir sie bereits in Beispiel q. erstellt haben, übernehmen wir sie einfach.
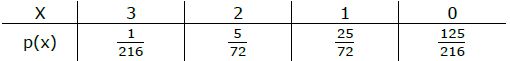
a) Nun kann man den Erwartungswert berechnen.
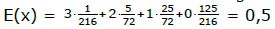
Der Schüler gewinnt im Schnitt 0,50€ pro Spiel [wir haben aber jedoch noch nicht darüber geredet, wie viel er pro Spiel zahlen muss!!!]
b) Wenn der Spieler im Durchschnitt 0,50€ gewinnt, dann müsste das Spiel natürlich genau 0,50€ kosten, um fair zu sein.
Beispiel u.
In einer Urne befinden sich 4 rote und 2 blaue Kugeln. Nun werden die Kugeln einzeln und ohne sie wieder zurück zu legen entnommen. Beim Ziehen einer roten Kugel muss der Spieler 6€ zahlen und er muss noch einmal Ziehen. Beim Ziehen einer blauen Kugel erhält der Spieler 9€ und das Spiel ist beendet.
a) Bestimmen Sie den Erwartungswert für die Anzahl der gezogenen Kugeln!
b) Mit welchen durchschnittlichen Gewinn oder Verlust muss der Spieler rechnen?
Lösung:
a) Um den Erwartungswert zu bestimmen, brauchen wir zuerst die Wahrscheinlichkeitstabelle.
Die hatten wir in Beispiel r. gemacht. Hier ist sie noch mal:
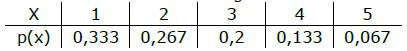
Nun kann man einfach den Erwartungswert berechnen.
E(X) = 1·0,333+2·0,267+3·0,2+4·0,133+5·0,067 = 2,334
Im Durchschnitt werden 2,334 Kugeln gezogen.
b) Ein durchschnittlicher Gewinn ist wieder ein Erwartungswert. Also geht’s genau gleich, nur nicht mit der Anzahl der gezogenen Kugeln, sondern eben mit dem Gewinn. Also erstellen wir wieder einen Wahrscheinlichkeitstabelle. Auch die haben wir in Beispiel r. bereits errechnet. Hier ist sie:

Nun kann man den Erwartungswert berechnen.
E(G) = 9·0,333+3·0,267+(-3)·0,2+(-9)·0,133+(-15)·0,067 = 0,996 ≈ 1€
Der Spieler gewinnt also tatsächlich, und zwar durchschnittlich ca. 1€ pro Spiel.
W.15.08 | Tschebyschew-Ungleichung
[Tschebyschew war Russe. Durch die Übersetzung der kyrillischen Buchstaben in unser Alphabet, taucht der Name auch in der Form: „Tschebyscheff“ oder „Tschebyschow“ oder … auf].
Die Tschebyschew-Ungleichung berechnet die Wahrscheinlichkeit, dass ein Ereignis um einen bestimmten Wert vom Erwartungswert abweicht.
Das Schöne daran ist, dass es für die Tschebyschew-Ungleichung völlig egal ist, um was für eine Verteilung es sich handelt [Binomialverteilung, Normalverteilung, ...], mit oder ohne Zurücklegen, … Alles egal.
Man braucht nur den Erwartungswert und die Standardabweichung!
Die Tschebyschew-Ungleichung:
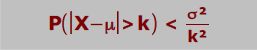
μ Erwartungswert
σ Standardabweichung
k die Abweichung von x zu μ
In Worten: Die W.S., dass ein Ereignis mehr als „k“ vom Erwartungswert abweicht, ist kleiner als 
Teilweise taucht die Formel in minimal geänderter Form auf: 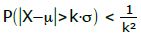
Diese Formel ist auch ganz toll, aber wir verfolgen sie nicht weiter [ohne besonderen Grund].
Beispiel u.
Bei einer Umfrage wird ein Mittelwert von μ=254 und eine Standardabweichung von σ=18. Mit welcher W.S. weicht ein beliebig ausgesuchter Wert um mehr als 30 vom Erwartungswert ab?
Lösung:
Wir setzen μ=254 und σ=18 in die Formel ein. Die Abweichung von 30 ist k.
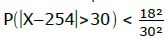
Nun einfach die rechte Seite errechnen.
P(|X–254|>39) < 0,36
Antwort: Mit einer W.S. von [höchstens] p=0,36?36% weicht ein beliebiger Wert der Umfrage um mindestens 30 ab.
Beispiel v.
Mit welcher W.S. weicht ein Ereignis um mehr als die anderthalbfache Standardabweichung vom Erwartungswert ab?
Lösung:
Wir kennen keine Zahlen, aber wenn man die Tschebyscheff-Ungleichung verwendet, ist die Aufgabe trotzdem einfach.
Der große Tschebyscheff sagte früher einmal: .jpg)
k ist die anderthalbfache Standardabweichung ⇒ k=1,5·σ
Setzt man k=1,5·σ in die Tschebyscheff-Ungleichung ein, erhält man:
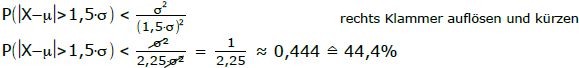
Antwort: Weniger als 44,4% aller Ereignisse weichen mindestens um die anderthalbfache Standardabweichung ab. [Von jedem Ereignis des Universums!]
Beispiel w.
In einem Casino wird an einem Spieltisch ein Würfel immer ca. 1200 mal geworfen.
Mit welcher W.S. werden zwischen 160 und 240 mal Sechser geworfen?
Lösung:
Zuerst machen wir uns klar, dass es sich um eine Binomialverteilung handelt.
Dadurch können wir recht einfach Erwartungswert und Standardabweichung berechnen [die W.S. für eine „6“ beträgt bekanntlich p(„6“)=1/6].
.jpg)
Die gesuchte Anzahl von 160 bis 240 Sechser liegt um den Wert von 40 um den Erwartungswert von μ=200 herum. Man könnte die Frage auch so stellen: Mit welcher W.S. weicht die Anzahl der Sechser um höchstens 40 vom Erwartungswert ab?
Man könnte die Frage auch so stellen: Mit welcher W.S. weicht die Anzahl der Sechsen um weniger als 40 vom Erwartungswert ab?
Wir berechnen nun zuerst über die Tschebyscheff-Ungleichung die W.S., dass die Abweichung vom Erwartungswert größer als 40 ist.

Die W.S., dass die Anzahl der Sechser um mehr als 40 vom Erwartungswert abweicht, ist kleiner als 0,104.
Daher ist die W.S., dass die Anzahl der Sechser um weniger als 40 vom Erwartungswert abweicht, ist größer als 1–0,104=0,896.
Die Wahrscheinlichkeit, dass die Anzahl der Sechser zwischen 160 und 240 liegt, beträgt 0,896, also 89,6%.


