Oberstufe

V.02 | Schnittmengen

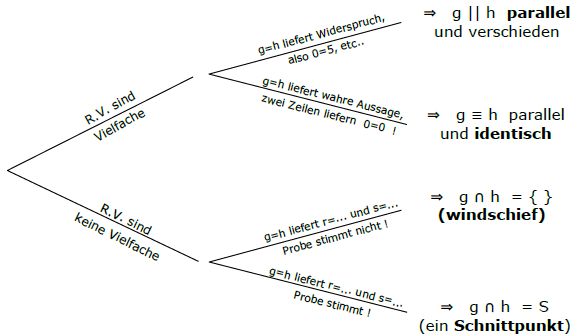
Schnittmengen zu berechnen, bedeutet Geraden und Ebenen auf Schnittpunkte und Schnittgeraden zu überprüfen. Dieses nennt man auch „gegenseitige Lage“ bestimmen.  Wichtig sind gegenseitige Lage von zwei Geraden, gegenseitige Lage einer Gerade mit einer Ebene und die gegenseitige Lage zweier Ebenen. Die gesuchten Lösungen (bzw. den Lösungvektor) berechnet man immer Gleichungen oder Gleichungssystemen.

 

Es wird ja immer wieder behauptet, Mathe hätte nicht so viel mit dem „richtigen“ Leben zu tun. Das ist natürlich völlig aus der Luft gegriffen und wirklich nicht wahr.
Zum Beispiel dreht sich in Mathe fast alles nur um das Eine (wie im richtigen Leben). In Mathe sind es Schnittpunkte und so Zeug. Welch Zufall, dass Schnittpunkte in Mathe manchmal auch Durchstoßpunkte heißen. (Ein Begriff, der die Fantasie ungeheuer anregt. Genau so wie der „Höhepunkt“ einer Kurve; zwei geometrische Figuren, die „sich decken“, wenn sie kongruent sind; etc...). Zurück zum Thema.
Wir waren also da stehengeblieben, dass sich auch in Mathematik alles um das Eine dreht, nämlich um Durchstoßpunkte Schnittpunkte.
Und wie im richtigen Leben, wo man auch nicht immer gleich zu der EINEN Sache kommt, sondern erst drum rum redet, wollen wir hier auch erst ein bisschen um die Theorie der Schnittmengen drumrumreden.

Wenn man zwei Sachen miteinander schneidet, erhält man immer eine Gleichung. Je nachdem, welche Form diese Gleichung hat, erkennt man (im Normalfall) schnell
1) ob sich die beiden Dinge schneiden,
2) ob sie ineinander liegen (identisch sind) oder
3) ob sie parallel zueinander sind.

Bei einer Gleichung, die einen Widerspruch liefert, also:
0 = 2, 2 = 4, r²<0, ...
gibt es keine Lösung. Egal an welcher Stelle der Rechnung man ist, man braucht nicht weiterrechnen. Auch ein paar Zeilen weiter unten wird nichts anderes rauskommen. Die beiden Dinge, die man geschnitten hat, sind parallel. ( Ausnahme: bei zwei Geraden könnte es auch „windschief“ sein. [hängt vom Richtungsvektor ab]).

Bei einer Gleichung, die eine wahre Aussage liefert, also:
0 = 0, 2 = 2, r²>0, ...
gibt es im Normalfall unendlich viele Lösungen. Im Normalfall heißt das: Falls es die einzige Gleichung der Rechnung ist, ist man fertig und hat eben ∞ (unendlich) viele Lösungen.
Die beiden Dinge, die man geschnitten hat, liegen ineinander (oder sind identisch).

Bei einer Gleichung, in der man nach der Unbekannten auflösen kann:
2^r=4, r–r–2=0, ...
gibt es ein oder zwei Lösungen (so viele, wie die Gleichung eben liefert) und genau so viele Schnittpunkte gibt es auch. (im Normalfall)

 

V.02.01 | Schnitt Gerade-Gerade (vier mögliche Lagen)

Geraden können auf vier Arten zueinander liegen:
1)    sie sind identisch,  d.h. sie haben ∞ viele Schnittpunkte, damit müssen beim Gleichsetzen ∞ viele Lösungen rauskommen.
2)    sie sind parallel und verschieden, d.h. es kommt keine Lösung raus.
3)    sie sind windschief. Auch hier kommt keine Lösung raus. (Den Unterschied zu parallel sieht man nur daran, dass beide Richtungsvektoren keine Vielfache voneinander sind).
4)    sie haben einen Schnittpunkt. Man erhält also eine Lösung für jeden Parameter.

 

Zur Vorgehensweise beim Gleichsetzen von Geraden:

⇒ Zuerst betrachtet man die Richtungsvektoren der Geraden und schaut ob sie Vielfache voneinander sind oder nicht.
    Sind sie Vielfache, so sind die Geraden parallel oder identisch.
    Sind die keine Vielfache, schneiden sich die Geraden oder sind windschief.

⇒ Die beiden Geraden gleichsetzen. Die drei Zeilen der Geraden liefern uns drei Gleichungen, aber nur zwei Unbekannte. (Normalerweise braucht man für zwei Unbekannte nur zwei Gleichungen).
    Danach werden wir folgendermaßen vorgehen:
    Wir errechnen aus den ersten beiden Gleichungen die Parameter r und s. Die dritte Gleichung verwenden wir nur um die Probe zu machen, d.h die Werte, die wir für die Parameter aus der ersten und zweiten Gleichung erhalten haben, setzen wir beide in die dritte Gleichung ein und hoffen so `was wie  „0=0“ zu erhalten.

 

 

Beispiel a.

Bestimme die Schnittmenge der Geraden g und h, mit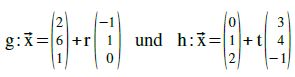  

Lösung:
Auf den ersten Blick erkennen wir natürlich, dass die Richtungsvektoren Vielfache voneinander sind. Die Geraden sind also entweder parallel [und verschieden]  oder identisch. Wir erwarten also entweder keine Lösung oder ∞ viele Lösungen.

 

 

Beispiel b.

Bestimmen Sie die gegenseitige Lage von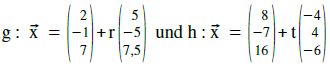 

Lösung:
Auf den ersten [oder zweiten] Blick erkennen wir natürlich, dass die Richtungsvektoren Vielfache voneinander sind [wenn man mit dem Taschenrechner: 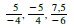 ausrechnet, kommt immer -1,25 raus.] Die Geraden sind also entweder parallel [und verschieden]  oder identisch.

Wir erwarten also entweder keine Lösung oder ∞ viele Lösungen.

 

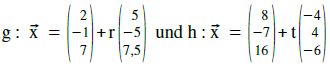
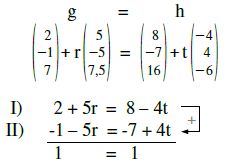
wahre Aussage. Jetzt auch noch erste mit dritter Gleichung überprüfen:

 

 

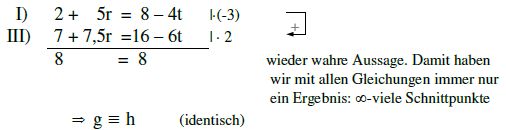
Beispiel c.

Wie werden wohl diese beiden Geraden zueinander liegen?

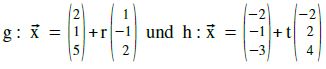
Lösung:
Auf den ersten Blick erkennen wir natürlich, dass die Richtungsvektoren keine Vielfache voneinander sind [die Vorzeichen sind falsch].
g und h  sind also entweder windschief oder haben einen Schnittpunkt.

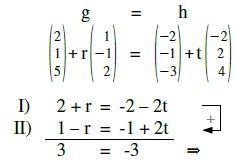
Widerspruch, g und h sind windschief!

 

Beispiel d.

Untersuchen Sie die beiden Geraden auf Schnittpunkte.

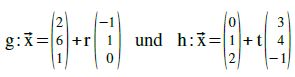
Lösung:
Die Richtungsvektoren sind keine Vielfache voneinander. g und h sind entweder windschief oder  haben einen Schnittpunkt. Wir erwarten also entweder keine oder eine Lösung.

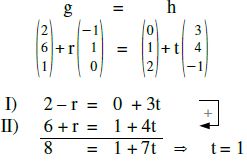
t=1 in I  [oder in II] einsetzen:   ⇒   2–r = 0+3·1   ⇒…⇒    r= -1

Probe:    [t = 1 und r = -1  in dritte Gleichung einsetzen]
        1+(-1)·0 = 2+1·(-1)
            1          =      1            ⇒            Probe stimmt. g und h schneiden sich!

Wo der Schnittpunkt liegt, erhält man, indem man   r in g   oder   t in h   einsetzt.

r = -1  in g : 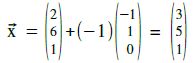 ⇒        S ( 3 | 5 | 1 )

 

 

Beispiel e.

Bestimmen Sie die Schnittmenge der beiden Geraden:

Lösung:
Sofort erkennt das geschulte Mathematikerauge die  Richtungsvektorenvielfach­heitalsodoppeltheit.
Die Geraden sind also entweder parallel (und verschieden)  oder identisch.
Wir erwarten also entweder keine Lösung oder ∞ viele Lösungen.

Dass in h kein Stützvektor steht, stört nicht. Man stellt sich einfach vor, es hieße: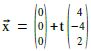 

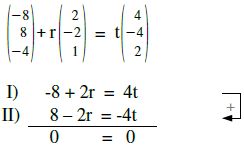
wahre Aussage. Jetzt auch noch erste mit dritter Gleichung überprüfen.

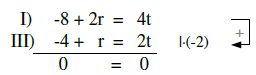
wieder wahre Aussage.

Wir haben alle drei Gleichungen verwendet und haben immer nur wahre Aussagen erhalten.            ⇒    g ≡ h    (g und h sind identisch)

 

 

Beispiel f.

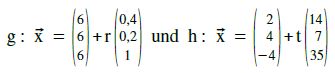
Lösung:
Auf den fünften Blick erkennen wir sofort, dass die Richtungsvektoren Vielfache voneinander sind 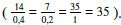  Beide Geraden sind also entweder parallel [und verschieden] oder identisch.  Wir erwarten also entweder keine Lösung oder ∞ viele Lösungen.

 

 

Beispiel g.

Was haben die beiden Geraden gemeinsam?

Lösung:
Die Richtungsvektoren sind keine Vielfache voneinander. g und h sind entweder windschief oder  haben einen Schnittpunkt. Wir erwarten also entweder keine oder eine Lösung, sie haben also entweder einen oder keinen Punkt gemeinsam.

 

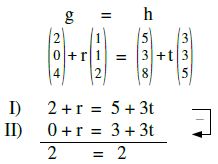
wahre Aussage.  Jetzt auch noch erste mit dritter Gleichung überprüfen.

 

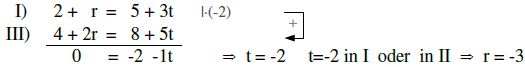
Wo der Schnittpunkt liegt, erhält man, indem man entweder „r“ in g  oder „t“ in h einsetzt.

„r=-3“ in g: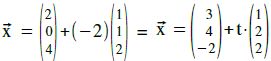  

⇒    Antwortsatz:      g und h haben den Punkt  S(-1|-3|-2)  gemeinsam.

 

Beispiel h.

Trägt die ∞ Liebe der beiden Geraden Früchte?

Lösung:
Die Richtungsvektoren sind keine Vielfache voneinander. g und h sind entweder windschief oder  haben einen Schnittpunkt. Wir erwarten also entweder keine oder eine Lösung.

 

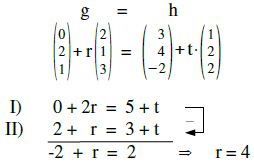     r=4   in I  oder  in II  ⇒  t = 3

Jetzt r = 4 und t = 3  in dritte Gleichung einsetzen (für Probe).

III)    1 +  4·3  = 1 + 3·1        Probe stimmt nicht. g und h schneiden sich nicht!
[Wir wissen zwar nicht, ob die ∞e Liebe von g und h Früchte trägt, aber sie haben nichts gemeinsam]
Antwortsatz:
Keine Hoffnung auf irgendeine Gemeinsamkeit von g und h.   -   Traurig.
(Die beiden Geraden sind windschief)

 

 

 

V.02.02 | Schnitt Gerade-Ebene (drei mögliche Lagen)

Das Allereinfachste auf der ganzen Welt ist es, Geraden mit Ebenen zu schneiden:
Man setzt die Gerade in die [Koordinatenform der] Ebene ein und löst nach dem Parameter auf.

Beispiel i.

Bestimme die Schnittmenge von  E : 4x₁–4x₂+2x₃=12  mit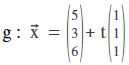 

Lösung:
Von der Gerade kennen wir x₁, x₂, x₃: 

Wenn wir diese x₁, x₂, x₃ in die Ebene einsetzen, erhalten wir:

    4·(5+t)–4·(3+t)+2·(6+t)=12

     20+2t=12   ⇒    t=-4

t=-4  in  g  ⇒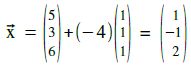 

 

Beispiel j.

Bestimme die Schnittmenge von  E : 2x₁–3x₂+4x₃=5  mit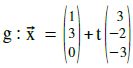 

Lösung:
x₁, x₂, x₃ setzen wir in die Ebene ein:
2·(1+3t) – 3·(3–2t) + 4·(-3t) = 5
                -7  =  12     ⇒   Widerspruch.
g und E schneiden sich also nicht. Sie müssen also parallel sein!        g || h

 

Beispiel k.

Bestimme die Schnittmenge von  E : 8x₁–4x2+x₃=5  mit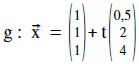 

Lösung:
Wir setzen x₁, x₂, x₃  von der Geraden in die Ebene ein:
        8·(1+0,5t) – 4·(1+2t) + (1+4t) = 5
                5     =    5                wahre Aussage
Es gibt ∞ viele Lösungen. g muss also in E enthalten sein.            g ⊂ E

 

Beispiel m.

Gegeben ist die Gerade  und die Ebene E : x₁–2x₂+3x₃=4

Bestimme die Parameter a und b so, dass
a) g und E parallel zueinander sind,
b) g in E enthalten ist,
c) g und E sich in einem Punkt schneiden !

Lösung:
Stellen Sie sich vor, wir hätten keine Parameter a und b.
Dann würden wir nach „t“ auflösen. Das machen wir jetzt auch hier, trotz Parameter.

Wir setzen die Gerade in die Ebene ein:
          (a+3t) – 2(1+bt) + 3(3+t) = 4
            a + 7 + 6t – 2bt = 4                   |a7
              t?(6–2b) = a–3

Jetzt sind wir mit dem rechnerischen Teil schon fertig und können bereits alles sehen, was wir brauchen.
Im Normalfall ergibt diese Gleichung eine Lösung [für t]: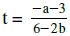 

Wir müssen uns aber auf jeden Fall noch überlegen, unter welchen Umständen diese Gleichung Sonderfälle (unendlich viele oder keine Lösung) liefert.
Eine Gleichung liefert unendlich viele Lösungen, wenn sie die Form „0=0“ hat.
Die Gleichung „t?(6–2b)=a–3“ hat aber nur dann die Form „0=0“, wenn 6–2b=0 ist und wenn a–3=0 ist. ( 6–2b=0 ⇒ b=3 und a–3=0 ⇒ a=3 )
Wir folgern also, dass die Gleichung ∞ viele Lösung hat, wenn b=3 und a=3

Eine Gleichung liefert keine Lösungen, wenn sie die Form „0=NichtNull“ hat.
Die Gleichung „t?(6–2b)=a–3“ hat aber nur die Form „0=NichtNull“,
wenn 6–2b=0 ist und wenn a–3≠0 ist. ( 6–2b=0 ⇒ b=3 und a–3 ⇒ ≠0 a ⇒ ≠3 )
Wir folgern also, dass die Gleichung keine Lösung hat, wenn b=3 und a≠3.

Zusammenfassung:
Für b=3 und a=3 gibt es unendlich viele Lösungen, g liegt also in E.
Für b=3 und a≠3 gibt es keine Lösung, g und E sind also parallel
Für b≠3 (alle anderen Fälle) gibt es eine Lösung, also einen Schnittpunkt.

 

Beispiel n.

Gegeben sind 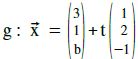 und E : 2x₁+ax2–2x3=3a

Bestimme die Parameter a und b so, dass
a) g und E parallel zueinander sind,
b) g in E enthalten ist,
c) g und E sich in einem Punkt schneiden !

Lösung:
Natürlich schneiden wir g und E wieder und lösen nach „t“ auf.

g in E:2?(3+t) + a?(1+2t) – 2?(bt) = 3a
6+2t + a+2at – 2b+2t = 3                     zusammenfassen
6+4t+a–2b+2at = 3a                            | 6–a+2b
4t+2at = 2a+2b–6                               ausklammern
t?(4+2a) = 2a+2b–6                             | :(4+2a)

Wie interpretieren wir dieses Ergebnis?

g liegt in E, wenn es unendlich viele Lösungen gibt.
Das ist der Fall, wenn die Gleichung die Form 0=0 hat, bei a=2 und b=5
( 4+2a=0 ⇒ a=2 und 2a+2b–6=0 ⇒ ... ⇒ b = 3a = 3(-2) = 5)

g und E sind parallel, wenn es keine Lösung gibt.
Das ist der Fall, wenn die Gleichung die Form 0=Zahl hat, bei a=2 und b≠5
( 4+2a=0 ⇒ a=2 und 2a+2b–6⇒≠0 ⇒ ...  ⇒ b ≠ 5)

g und E haben einen Schnittpunkt, wenn es eine Lösung gibt.
Das ist der Fall, wenn die Gleichung die Form Zahl?t=Zahl hat, bei a≠2.

 

Man kann zwei Ebenen gut miteinander schneiden, wenn beide in Koordinatenform sind oder eine in Koordinatenform und die andere in Parameterform (=Vektorform).
Wenn beide in Parameterform gegeben sind, empfiehlt es sich eine oder beide in Koordinatenform umzuwandeln.

Beispiel o.

Bestimme die Schnittgerade der Ebenen E₁ : 2x₁+3x₂–x₃=6 und E2 : x₁+x₂–2x₃=2

Lösung:
Bei zwei Koordinatengleichungen schreibt man die beiden Gleichungen untereinander und verrechnet sie derart, dass ein x₁ x₂ oder x₃ weg fällt. Nehmen wir einfachheitshalber an, x₁ würde wegfallen.
Es bleiben also x₂ und x₃ übrig. Nun setzt man x₂ oder x₃ gleich „t“ und versucht nun auch x₂ und x₁ in Abhängigkeit von „t“ zu erhalten. Dann ist man mehr oder weniger fertig.

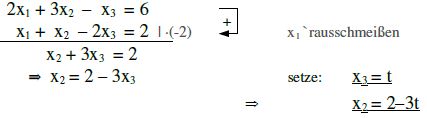
x₂ und x₃ in eine der beiden Ebenengleichungen einsetzen..

2?x₁ + 3?(2–3t) – t = 6
2x₁ + 6 – 9t – t = 6
2x₁ = 10t      ⇒     x₁ = 5t

Nun suchen wir ja eine Schnittgerade.

?Geraden haben immer die Form: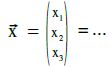 

Wir können also x₁ x₂ x einsetzen und erhalten:

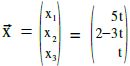 = [Vektor aufspalten] =  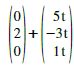 = [t ausklammern] =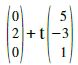 

 

Die Gleichung der Schnittgeraden lautet: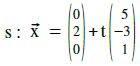 

 

Beispiel p.

Bestimmen Sie die Schnittgerade !

E₁ : 2x₁–3x₂–x₃ = 2 und E2 :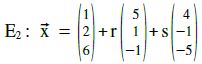 

Lösung:
Wenn eine Ebenengleichung in Koordinatenform und die andere in Parameterform gegeben ist, gehen wir ähnlich vor, wie bei Schnitt GeradeEbene. Wir setzen die Parameterform in die Koordinatenform ein und lösen nach „r“ oder „s“ auf.
Dieses [r oder s] setzen wir dann wieder in die Parameterform ein, [wo es herkommt].

   

 

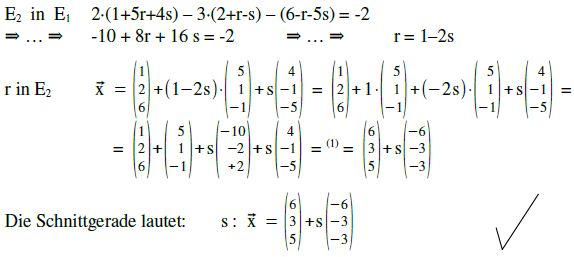
Beispiel p.

Bestimmen Sie die Parameter „a“ und „b“ so, dass die Ebenen
E : 2x₁ + ax₂ – 4x₃ = 5 und F : x1 + 4x₂ + bx₃ = 8      parallel sind !

Lösung:
Damit E und F parallel sind, müssen die beiden Normalenvektoren vielfach sein.

Fertig!

 

Beispiel q.

Sei E : x₁ + 3x₂ – 2x₃ = 2 und F : (k+1)x₁ + (2k+4)x₂ + (3–k²)x₃ = 5–k
Bestimme „k“ so, dass die Ebenen E und F identisch sind.

Lösung:
Damit die Ebenen identisch sind, müssen die Normalenvektoren Vielfache voneinander sein.
Zusätzlich müssen die rechten Seiten dann auch passen [die gleichen Vielfache sein], aber darum kümmern wir uns erst am Schluss.

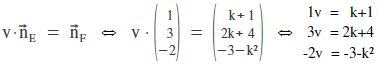
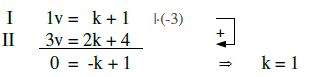
Man könnte wieder die Probe machen, indem man v ausrechnet und dann v und k in die dritte
Gleichung einsetzt. Ich setze k jedoch gleich in die Ebenengleichung von F ein, damit sieht man dann
auch gleich, ob die rechten Seiten übereinstimmen.

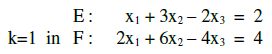
Beide Ebenen sind perfekt gleich [genau das Doppelte voneinander],
damit sind sie identisch.