Oberstufe
V.03 | Abstände
Es gibt drei wichtige Abstände: 1.Abstand Punkt-Punkt, 2.Punkt-Gerade, 3.Abstand Punkt-Ebene. Die Entfernung von allem anderen führt man auf diese ersten drei zurück. (Ausnahme bilden zwei windschiefe Geraden. Man kann deren Abstand berechnen, in dem man entweder eine Formel anwendet oder die Lotfußpunkte bestimmt.)
In eine Prüfung in Mathe zu gehen, ohne Abstand PunktPunkt, Abstand PunktEbene oder PunktGerade zu können, ist derart sinnlos, dass Sie stattdessen daheim bleiben und sich einen schönen Tag machen können.
V.03.01 | Abstand Punkt-Punkt berechnen
Beispiel a.
Bestimmen Sie den Abstand von A( 4 | 2 | 1 ) zu B( 1 | 3 | 6 ) !
Lösung:
⇒ Verbindungsvektor AB aufstellen: 
⇒ Länge des Vektors bestimmen: 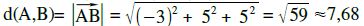
Beispiel b.
Bestimme den Abstand der Punkte A und B mit: A(1|2|3) und B(4|0|4).
Lösung:d(A,B) = 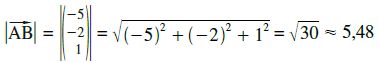
Beispiel c.
Bestimme den Parameter „k“ so, dass der Abstand von C( 8 | 3 | 6 ) zu D( k | 5 | 4 ) 18LE beträgt !
Lösung:
d(C,D) = 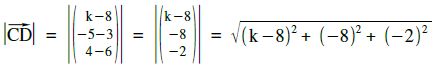
Falls man einen GTR/CAS verwenden darf, kann man ab hier diese Gleichung von ihm lösen lassen. Wir rechnen jedoch natürlich lieber alles mühsam von Hand. Masochismus pur!
Dieser Abstand soll nun den Wert 18 annehmen, es gilt also:
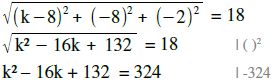
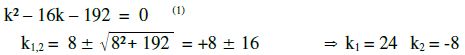
Beispiel d.
Welche Punkte der Gerade  haben von P( 4 | 3 | 2 ) den Abstand 6 ?
haben von P( 4 | 3 | 2 ) den Abstand 6 ?
Lösung:
Immer, wenn man von einem Punkt nur weiß, dass er auf einer Gerade liegt, bekommt er die „Koordinaten“ von dieser Gerade [nennt sich auch „laufender Punkt einer Geraden“ oder „Einzelpunktform“ einer Gerade] [x1=-1+1·t, x2=2-1·t, x3=-6+4·t].
Jeder Punkt von g hat also die Koordinaten: G( -1+t | 2–t | -6+4t )
Nun rechnen wir ganz stupide den Abstand von G zu P aus.
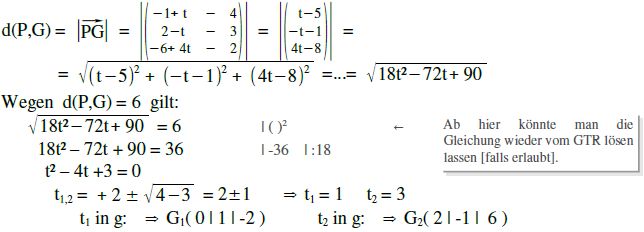
V.03.02 | Abstand Punkt-Gerade über Lotebene berechnen
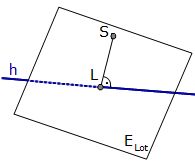
Um den Abstand Punkt-Gerade zu bestimmen, werden wir:
→ erst die Lotebene ELot aufstellen,
→ dann den Lotfußpunkt L [als Schnittpunkt von ELot mit h] bestimmen,
→d ann den Abstand von L zum gegebenen Punkt.
Beispiel e.
Der Vogel „Schlumpi“ befindet sich im Punkt S(15|4|-2). Er ist sehr müde.
Da sichtet er plötzlich eine Hochspannungsleitung, welche entlang der Geraden 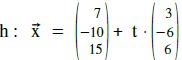 verläuft.
verläuft.
Wie weit muss Schlumpi noch fliegen, um sich auf der Hochspannungsleitung ausruhen zu können ?
Lösung:
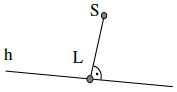
Erstmal bestimmen wir den Punkt L der Hochspannungsleitung, welcher von Schlumpi aus gesehen, am nächsten liegt. [Unromantiker würden sagen: wir errechnen den Lotfußpunkt.] Dazu stellen wir in Gedanken eine Ebene auf, welche senkrecht zur Hochspannungsleitung liegt und durch Schlumpi geht. [Natürlich tut das Schlumpi nicht weh, es ist ja nur eine imaginäre Ebene.] Der Normalenvektor dieser Ebene müsste also der Richtungsvektor der Hochspannungsleitung h sein.
Wir wissen also: diese [imaginäre!] Lotebene hat die Form: ELot : 3x1–6x2+6x3=d
Da ELot durch Schlumpi geht [ohne ihm weh zu tun!!] kann man mit diesem Punkt S eine Punktprobe machen, man kann also S in ELot einsetzen.
S in ELot : 3·15–6·4+6·(-2)=d ⇒ d=9
Unsere Lotebene lautet also ELot : 3x1–6x2+6x3=9
Nun schneiden wir diese Lotebene [welche Schlumpi wirklich überhaupt nicht weh tut] mit der Hochspannungsleitung h und erhalten den Lotfußpunkt L [Schlumpis Ausruhpunkt].
h ∩ Elot : 3·(7+3t)–6·(-10–6t)+6·(15+6t)=9
171+81t=9 ⇒ t=-2 t in h ⇒ L (1|2|3)
„Schlumpi, flieg so schnell Du kannst zum Punkt L(1|2|3). Dahin ist es am kürzesten !“
Wir berechnen derweil, wie weit es wirklich ist.
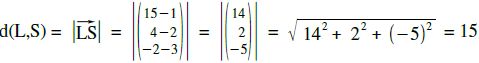
Schlumpi muss noch 15 Längeneinheiten fliegen.
[Während der vielen Minuten, die wir für diese Rechnung gebraucht haben, hat sich Schlumpi auf dem Boden ausgeruht und wurde derweil leider vom Fuchs gefressen.]
V.03.03 | Punkt-Gerade über laufenden Punkt
Mal schauen, ob wir die „Schlumpi“-Aufgabe auch anders lösen können.
Beispiel f.
Der Vogel „Schlumpi2“ befindet sich im Punkt S(15|4|-2). [Schlumpi1 wurde ja vom Fuchs gefressen.]
Auch er ist sehr müde. Da sichtet er plötzlich wieder die Hochspannungsleitung, welche entlang der Geraden 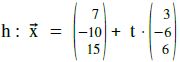 verläuft.
verläuft.
Wie weit muss Schlumpi2 noch fliegen, um sich auf der Hochspannungsleitung ausruhen zu können ?
Lösung:
Wir probieren folgenden Ansatz: Da der Lotfußpunkt L sich auf der Geraden h befindet, hat er die Koordinaten L( 7+3t | -10–6t | 15+6t ).
Da L ein Lotfußpunkt ist, steht der Vektor SL senkrecht auf der Geraden h.
Wie wir aus V.05.02 wissen, gibt das Skalarprodukt von zwei Vektoren, die senkrecht aufeinander stehen, Null. Das bedeutet, dass auch das Skalarprodukt von SL mit dem Richtungsvektor von h Null ergeben muss.
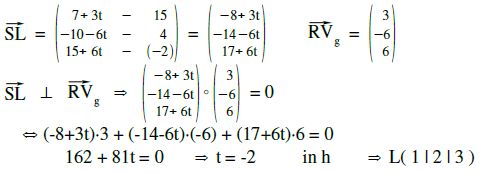
Der gesuchte Abstand von Punkt S zur Gerade h ist gleich dem Abstand vom Punkt P zum Lotfußpunkt L.
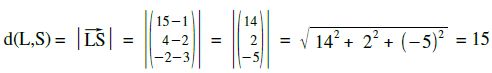
Schlumpi2 muss auch wieder 15 Längeneinheiten fliegen.
[Da wir nicht so viel gelabert haben wie in Bsp.5, hat es Schlumpi2 mit heiler Haut auf die Hochspannungsleitung geschafft.]
V.03.04 | Punkt-Gerade über laufenden Punkt (GTR)
Dieses Kapitel beachten Sie bitte nur, falls Sie einen GTR oder einen CAS verwenden dürfen. Falls ja, haben Sie Glück, denn der GTR liefert die schnellste Methode für die Abstandberechnung von einem Punkt zu einer Gerade.
Beispiel g.
Der Vogel „Schlumpine“ befindet sich im Punkt S(15|4|-2). [Schlumpine war die Freundin von Schlumpi1] Sie ist ein bisschen müde.
Plötzlich sichtet sie die gleiche Hochspannungsleitung, welche entlang der Geraden 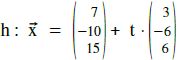
Wie weit muss Schlumpine noch fliegen, um sich auf der Hochspannungsleitung ausruhen zu können ??
Lösung:
Der Ansatz geht wieder über den laufenden Punkt der Geraden.
L( 7+3t | -10–6t | 15+6t ).
Der Abstand eines Punktes zur Geraden ist immer der kleinste Abstand.
Also berechnen wir jetzt einfach den Abstand von S zu L [in Abhängigkeit von t] und bestimmen davon das Minimum mit dem Taschenrechner.
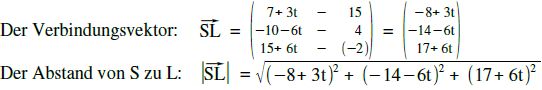
Diese lange Wurzel geben wir [so wie sie ist] in den GTR oder CAS ein und bestimmen davon das Minimum.
Möglichkeit 1: Man gibt sie im Grafik-Menü als Funktion ein und lässt sich das Minimum berechnen
oder
Möglichkeit 2: Je nach GTR-Modell erhält man im Hauptmenü über den „fMin“-Befehl das Minimum)
Man erhält ein Minimum bei x bzw. t=-2 und bei y bzw. d=15
In dieser Aufgabe war nur der Abstand gefragt, den haben wir nun. d=15
Wollte man auch noch den Lotfußpunkt haben, könnte man nun t=-2 in L(7+3t|-10–6t|15+6t) einsetzen und hätte den Lotfußpunkt L(1|2|3).
V.03.05 | Punkt-Gerade über sin(alpha)
Beispiel h.
Der Vogel „Schlumpus“ fliegt entlang der Geraden 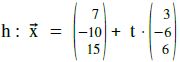
[Schlumpus ist der neue Freund von Schlumpine].
Schlumpus ist voll auf Speed, weil er gleich sein erstes Rendezvous mit seiner neuen Flamme hat. Seine Hormonproduktion läuft auf 200%.
Während er so fliegt, fällt ihm ein, dass er keine Kondome dabei hat.
Ein entsprechender Automat befindet sich im Punkt K(15|4|-2).
Wie weit ist der Automat von seiner Flugbahn entfernt ?
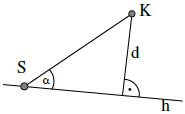
Lösung:
Schlumpus befindet sich irgendwo auf der Gerade.
Nehmen wir an, es wäre der Stützvektor S(7|-10|15).
Nun entsteht ein Dreieck, in welchem der gewünschte Abstand vom Punkt zu Geraden die Gegenkathete eines rechtwinkligen Dreiecks ist.
Es gilt: 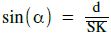
Berechnung der Hypotenusenlänge SK :

Berechnung des Winkels zwischen SK und Gerade.
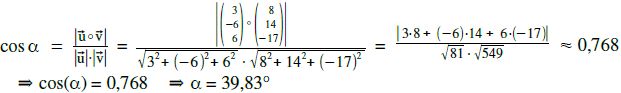
Berechnung des gesuchten Abstands Punkt-Gerade:
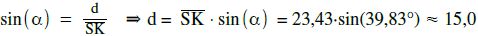
Der Abstand von Schlumpus´ Flugbahn zum Kondomautomaten beträgt 15m.
V.03.06 | Punkt-Ebene über Lotgerade
Wir stellen immer zuerst die Lotgerade gLot auf, dann errechnen wir den Lotfußpunkt L [als Schnittpunkt von gLot mit E].
Der gesuchte Abstand ist dann der Abstand von L zum gegebenen Punkt.
[Abstand Punkt-Ebene geht über Hesse-Normal-Form HNF aber immer schneller.]
Beispiel i.
Bestimme den Abstand von P(7|8|9) zu E : 4x1+4x2–2x3=6
Lösung:
Wir werden die Lotgerade auf E durch P bestimmen, um den Lotfußpunkt zu erhalten.
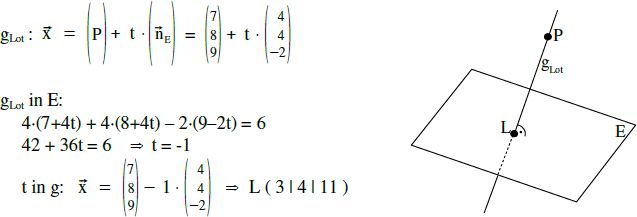
Der Abstand von L zu P ist gleichzeitig der gesuchte Abstand von E zu P !
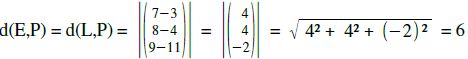
V.03.07 | Punkt-Ebene über HNF (Hesse-Normal-Form)
Es gibt mehrere Möglichkeiten die HNF (Hesse-Normal-Form) einer Ebene aufstellen. Eine davon halte ich persönlich für am einfachsten.
Man braucht dafür die Koordinatengleichung der Ebene, bringt alles nach links [so dass also rechts „0“ steht] und teilt nun durch den Betrag des Normalenvektors.
Beispiel j.
Es sei eine Ebene E : 2x1+2x2–x3=6

oder ein anderes Beispiel:
Es sei eine Ebene F : 6x1–2x2+3x3=-18
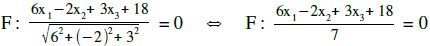
Um nun den Abstand irgendeines Punktes zu irgendeiner Ebene zu berechnen, nimmt man die HNF der Ebene, setzt den Punkt für x1, x2, x3 ein und erhält auf der rechten Seite statt „=0“ den Abstand Punkt-Ebene [also „d(E,P)“].
Weil Abstände immer positiv sind, wird das Ganze noch in Betrag gesetzt.
Beispiel k.
Bestimmen Sie den Abstand von P(7|8|9) zu E : 4x1+4x2–2x3=9
Lösung:
HNF der Ebene aufstellen
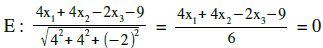
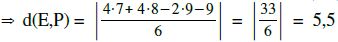
Beispiel m.
Welche Ebene ist parallel zu F : 4x1–7x2–4x3=0 und hat von Ü(6|6|6) den Abstand d=9?
Lösung:
Wenn die Ebene parallel zu F sein soll, hat sie den gleichen Normalenvektor, hat damit die Form:
E : 4x1–7x2–4x3=d besser: E : 4x1–7x2–4x3 = a
HNF der Ebene aufstellen 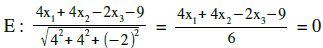
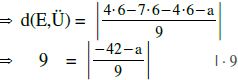
[Ab hier könnte man die Gleichung wieder vom GTR lösen lassen.]
81 = |-42–a| ← den Betrag löst man auf, indem
±81 = -42–a auf die andere Seite ein „±“ kommt.
81= -42–a ⇒ 123 = -a ⇒ a1=-123
-81= -42–a ⇒ -39 = -a ⇒ a2= 39
Die gesuchten Ebenen sind damit: E1 : 4x1–7x2–4x3 =-123
Beispiel n.
Sei  und E : 3x1+3x3+12=0
und E : 3x1+3x3+12=0
Welche Punkte der Gerade g haben von E den Abstand d= 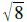
Lösung:
Jeder Punkt der Gerade hat die Koordinaten G( 10+7t | 7+2t | -2+t ).
Mit diesem miesen, fiesen, allgemeinen Punkt stellen wir den Abstand zur Ebene E auf und setzen ihn dann gleich 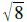 . [Und lösen dann nach „t“ auf].
. [Und lösen dann nach „t“ auf].
HNF der Ebene aufstellen 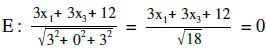
Um den Abstand zu berechnen: G in HNF einsetzen.
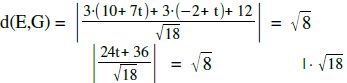
[Ab hier könnte man die Gleichung wieder vom GTR lösen lassen.]
|24t+36| = 12 Betrag auflösen
24t+36 = ±12
24t+36 = +12 ⇒ t1=-1
24t+36 = -12 ⇒ t2=-2 t1 und t2 wieder in g einsetzen
⇒ G1 ( 3 | 5 | -3 ) ⇒ G2 ( -4 | 3 | -4 )
V.03.08 | Parallele Geraden, Gerade-Ebene, Ebene-Ebene
→ Zwei parallele Geraden haben überall den gleichen Abstand. Man führt die Rechnung auf „Abstand Punkt-Gerade“ zurück. Man nimmt von der einen Gerade einen Punkt [z.B. den Stützvektor] und berechnet den Abstand zur anderen Geraden.
- Eine Ebene und eine Gerade, die zueinander parallel sind, haben überall den gleichen Abstand [na, kommt Ihnen das bekannt vor?]. Man führt alles auf die Berechnung von Punkt-Ebene zurück. Man nimmt von der Geraden einen Punkt [z.B. den Stützvektor] und berechnet den Abstand zur anderen Geraden.
- Zwei parallele Ebenen haben überall den gleichen Abstand [na, kommt Ihnen das bekannt vor?]. Man führt alles auf die Berechnung von Punkt-Ebene zurück. Man nimmt von der einen Ebene einen Punkt [z.B. einen Spurpunkt] und berechnet den Abstand zur anderen Ebene.
Beispiel n.
Sei 
Bestimmen Sie den Abstand beider Geraden.
Lösung:
Dass es sich um zwei parallele Geraden handelt, sieht man an den Richtungsvektoren. Damit ist der Abstand zwischen beiden Geraden überall gleich. Wir können also den Abstand von einem der beiden Stützvektor zur anderen Geraden berechnen.
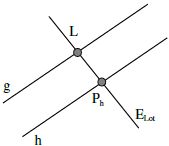
Wir wenden hier die Methode über die Lotebene an.
Wir können beispielsweise den Abstand von der Gerade g zum Stützvektor von h ausrechnen.
Den Stützvektor von h nennen wir mal Ph, er hat die Koordinaten: Ph(5|1|8)
Wir stellen zuerst die Lotebene auf, die senkrecht auf g steht und durch Ph geht.
ELot : 4x1+3x2+x3 = d
Ph in ELot : 4·5+3·1+8 = d ⇒ d=31 ⇒ ELot : 4x1+3x2+x3 = 31
Da wir fu?r die Lotebene den Stu?tzvektor von h genommen haben, schneiden wir ELot mit g!
ELot ∩ g: 4?(7+4t) + 3?(8+3t) + (5+t) = 31
57 + 26t = 31⇒t = 1
t in g ⇒ Lotfußpunkt L( 7–1?4 | 8–1?3 | 5–1?1 ) ⇒ L( 3 | 5 | 4 )
d(g,h) = d(L,Ph) = 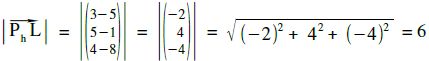
Beispiel n.
Sei 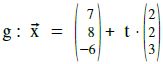 und E : 2x1+4x2–4x3=16
und E : 2x1+4x2–4x3=16
Bestimmen Sie den Abstand von g und E !
Lösung:
Da g und E parallel sind [das Skalarprodukt von 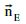 mit dem RVg ist Null], kann man einfach den Abstand vom Stützvektor zur Ebene ausrechnen.
mit dem RVg ist Null], kann man einfach den Abstand vom Stützvektor zur Ebene ausrechnen.
Beispiel o.
Sei E : 3x1+2x2+5x3=66 und F : 6x1+4x2+10x3=-50
Bestimmen Sie den Abstand der Ebenen E und F !
Lösung:
Da E und F parallel sind [beide Normalenvektoren sind Vielfache], kann man einfach den Abstand von irgend einem Punkt der einen Ebene zur anderen Ebene berechnen.
Irgendein Punkt der Ebene E ist z.Bsp. der Spurpunkt (22|0|0).
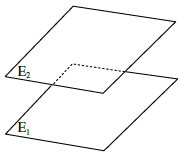
Der Abstand der beiden Ebenen ist überall gleich. Man nimmt irgend einen Punkt der einen Ebene und berechnet den Abstand zur anderen Ebene.
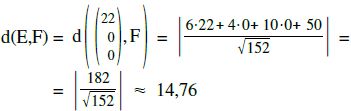
Es gibt mehrere Methoden, den Abstand zweier windschiefen Geraden zu berechnen.
Eine Methode [siehe Kapitel V.03.10] besteht darin, die Lotfußpunkte zu berechnen. Das dauert zwar etwas länger, aber es gibt viele Aufgaben, in welchen man die Lotfußpunkte tatsächlich braucht.
Die zweite Methode [Kapitel V.03.09] geht über die „einfache“ Formel: 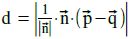
Das geht zwar schneller, hat aber manchmal den Nachteil, dass man die Lotfußpunkte nicht erhält.
Fazit:
Wenn man die Lotfußpunkte braucht, ist V.03.10 angebracht.
Wenn man die Lotfußpunkte nicht braucht, ist V.03.09 besser.
V.03.09 | Abstand windschiefer Geraden über Formel

Beispiel p.
Sei 
Bestimmen Sie den Abstand von g und h !
Lösung:
Da die Lotfußpunkte nicht gefragt sind, verwenden wir die Formel: 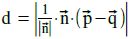
p und q sind die Stützvektoren der beiden Geraden.
Zuerst berechnen wir den Normalenvektor aus den beiden Richtungsvektoren der zwei Geraden.
[Ohne triftigen Grund verwenden wir die Methode vom Skalarprodukt. Die Methode über das Kreuzprodukt wäre natürlich besser]
V.03.10 | Abstand windschiefer Geraden berechnen über Berechnung der Lotfußpunkte
Beispiel r.
Sei 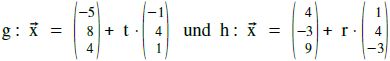
Welche Punkte der Geraden g und h haben den geringsten Abstand voneinander?
Bestimmen Sie den Abstand von g und h !
Lösung:
Wir werden so vorgehen: Stellt Sie sich eine Gerade vor, die sowohl g als auch h in einem rechten Winkel schneidet. Die Länge von dieser Verbindungsstrecke (in der Zeichnung 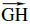 ) wäre der Abstand der beiden Geraden. Wir werden also G und H bestimmen, die Anfangund Endpunkt dieser senkrechten Verbindungsgeraden sind.
) wäre der Abstand der beiden Geraden. Wir werden also G und H bestimmen, die Anfangund Endpunkt dieser senkrechten Verbindungsgeraden sind.
Die Punkte sind die Lotfußpunkte und ich nenne sie analog zu ihren Geraden: „G“ und „H“.
Von G und H wissen wir nur, dass sie auf den Geraden g und h liegen, daher „geben wir“ G und H die Koordinaten der Geraden g und h: G( -5t | 8+4t | 4+t ) H( 4+r | -3+4r | 9-3r )
Unser Vektor 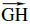 sieht demnach so aus:
sieht demnach so aus: 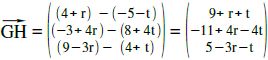
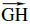 muss ja nun sowohl auf der Geraden g, als auch auf der Geraden h senkrecht stehen, deswegen muss das Skalarprodukt von
muss ja nun sowohl auf der Geraden g, als auch auf der Geraden h senkrecht stehen, deswegen muss das Skalarprodukt von 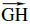 sowohl mit dem Richtungsvektor von g, als auch das mit dem Richtungsvektor von h Null ergeben.
sowohl mit dem Richtungsvektor von g, als auch das mit dem Richtungsvektor von h Null ergeben.
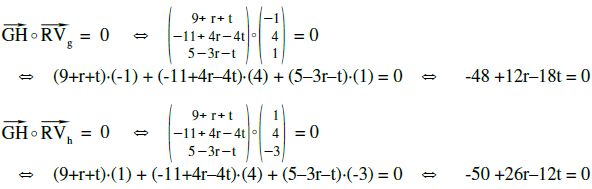
Aus diesen beiden Gleichungen berechnen wir „r“ und „t“.
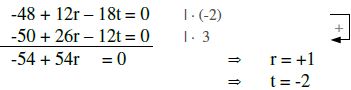
r und t zuru?ck in G und H eingesetzt, ergibt: G( -3 | 0 | 2 ) H ( 5 | 1 | 6 )
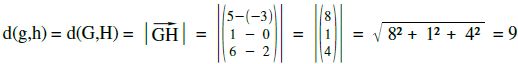
Beispiel s.
Sei 
Bestimmen Sie den Abstand von g und h !
Lösung:
G und H „geben wir“ wieder die Koordinaten der Geraden g und h, also: G( -4+3t | 2+2t | 20-6t ) H( 3 | -3+r | 9-2r )

Unser Vektor GH sieht demnach so aus:
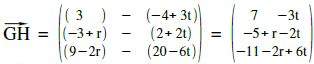
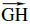 muss auf beiden Geraden senkrecht stehen, damit muss das Skalarprodukt
muss auf beiden Geraden senkrecht stehen, damit muss das Skalarprodukt
mit beiden Richtungsvektoren Null ergeben.
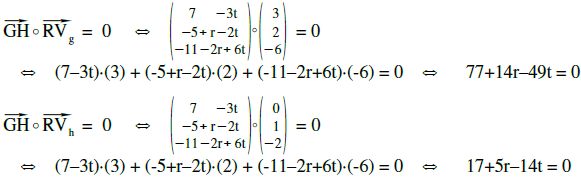
Aus diesen beiden Gleichungen berechnen wir „r“ und „t“.
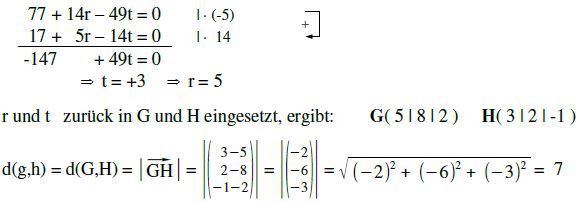
Verwandte Kapitel:
V.03 | Abstände
- V.03.01 | Punkt-Punkt
- V.03.02 | Punkt-Gerade über Lotebene
- V.03.03 | Punkt-Gerade über laufenden Punkt
- V.03.04 | Punkt-Gerade über laufenden Punkt (GTR)
- V.03.05 | Punkt-Gerade über sin(alpha)
- V.03.06 | Punkt-Ebene über Lotgerade
- V.03.07 | Punkt-Ebene über HNF (Hesse-Normal-Form)
- V.03.08 | Parallele Geraden, Gerade-Ebene, Ebene-Ebene
- V.03.09 | Abstand windschiefer Geraden ueber Formel
- V.03.10 | Abstand windschiefer Geraden über Lotfußpunkte


