Oberstufe
A.17 | Symmetrie
Funktionen können zwei Typen von Symmetrie aufweisen: Punktsymmetrie oder Achsensymmetrie zu einer senkrechten Achse. (Eine Funktion kann zu waagerechten Geraden nicht symmetrisch sein!)
Es gibt zwei Arten von Symmetrie: Punktsymmetrie und Achsensymmetrie.
Eine Funktion ist punktsymmetrisch, wenn es einen irgendeinen Punkt gibt, an dem man die Funktion derart spiegeln kann, dass als Spiegelbild wieder die gleiche Funktion rauskommt.
Eine Funktion ist achsensymmetrisch, wenn es eine Gerade [also eine Achse] gibt, an der man die Funktion derart spiegeln kann, dass als Spiegelbild wieder die gleiche Funktion rauskommt.

zwei achsensymmetrische Funktionen zwei punktsymmetrische Funktionen keine Symmetrie
Normalerweise interessiert man sich bei Symmetrie nur für Punktsymmetrie zum Ursprung und für Achsensymmetrie zur y-Achse.
Um die Symmetrie einer Funktion nachzuweisen gibt es zwei Formeln:

[A.17.01] Symmetrie für Weicheier
Bei ganzrationalen Funktionen schaut man nur auf die Hochzahlen von „x“.
Gibt es nur gerade Hochzahlen, ist f(x) symmetrisch zur y-Achse.
Beispiele: f(x) = 2x6–2,5x4–5 g(x) = 0,3x-2–3tx2 + 6t²x4
Gibt es nur ungerade Hochzahlen, ist f(x) symmetrisch zum Ursprung.
Beispiele: ht(x) = 2x5+12x3–2x i(x) = 2x-1+¶x-3–3¶²x-5+ x³–4x
Gibt es gemischte Hochzahlen, ist f(x) nicht symmetrisch.
Beispiele: j(x) = x3+2x2–3x+4 k(x) = 2x·(x³+6x²+9x)
[A.17.02] Symmetrie am Ursprung -- Symmetrie an y-Achse
Um die Symmetrie einer Funktion nachzuweisen, gibt es zwei Formeln:
f(-x) = f(x) ⇒ Achsensymmetrie zur y-Achse
f(-x) = -f(x) ⇒ Punktsymmetrie zum Ursprung
Man wendet die Formel folgendermaßen an:
Man setzt in die Funktion, die man überprüfen will, statt dem „x“ ein „(-x)“ ein (man berechnet also f(-x)). Danach vereinfacht man die Funktion.
Wenn nun wieder die Funktion f(x) rauskommt, hat man eine Achsensymmetrie zur y-Achse und ist natürlich fertig.
Sollte nicht wieder f(x) rauskommen, kann man noch ein Minus ausklammern, um zu schauen, ob man vielleicht -f(x) erhält. Wenn auch das nicht der Fall ist, ist f(x) weder zum Ursprung noch zur y-Achse symmetrisch und man geht frustriert heim.
Beispiel a. (= Beispiel einer Symmetrie zur y-Achse)
ft(x) = 2x6–2,5x4–5
f(-x) = 2(-x)6–2,5(-x)4–5 = 2x6–2,5x4–5 = f(x)
⇒ Achsensymmetrie zur y-Achse
Beispiel b. (= Beispiel einer Symmetrie zum Ursprung)
f(x) = 2x5+12x3–2x
f(-x) = 2·(-x)5+12·(-x)3–2·(-x) =
= 2·(-x5)+12·(-x3)+2·x =
= -2x5–12x3+2x =
[Es ist keine Achsensymmetrie, da nicht f(x) rausgekommen ist. Wir klammern jetzt ein Minus aus, um zu prüfen, ob´s vielleicht punktsymmetrisch ist.]
= -(2x5+12x3–2x) =
= - ( f(x) )
⇒ Punktsymmetrie zum Ursprung
Beispiel c. (= Beispiel einer Funktion ohne Symmetrie)
f(x) = x3 + 2x2 – 3x + 4
f(-x) = (-x)3+2(-x)2–3(-x)+ 4 =
= -x³ + 2·x2 + 3x + 4 =
[≠f(x), also „-“ ausklammern]
= -(x³ –2x2 – 3x – 4)
In der Klammer steht wieder nicht genau f(x).
Die Funktion ist also weder zum Ursprung, noch zur y-Achse symmetrisch.
Beispiel d. (= Beispiel einer Symmetrie zur y-Achse)
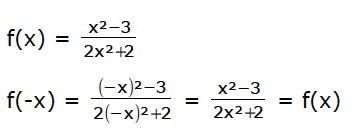
Beispiel e. (= Beispiel einer Symmetrie zum Ursprung)
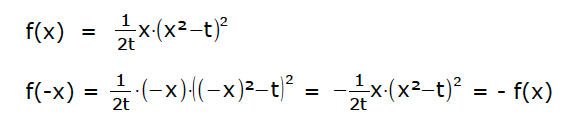
[A.17.03] Symmetrie über Formeln
Ist eine Funktion symmetrisch zu irgendeinem Punkt mit den Koordinaten S(a|b), so gilt die Formel: f(a–x)+f(a+x) = 2·b
Ist eine Funktion symmetrisch zu irgendeiner senkrechten Gerade mit der Gleichung x=a, so gilt: f(a–x) = f(a+x)
[Man setzt a,b und die Funktion f(x) in die Formel ein, löst alle Klammern etc.. auf und erhält zum Schluss eine wahre Aussage. Die Rechnungen sind oft aufwändig.]


[A.17.04] Symmetrie über Verschieben
Wenn eine Funktion symmetrisch zu irgendeinem Punkt ist, verschiebt man die Funktion so weit nach links/rechts und oben/unten, bis der Symmetriepunkt im Ursprung liegt. Nun kann man für die neue, verschobene Funktion Symmetrie zum Ursprung nachweisen [einfach über f(-x)=-f(x)].
Wenn eine Funktion symmetrisch zu irgend einer Achse ist, verschiebt man die Funktion so weit nach links/rechts, bis die Symmetrieachse auf der y-Achse liegt. Nun kann man für die neue Funktion Symmetrie zur y-Achse nachweisen [einfach über f(-x)=f(x)].
Nehmen wir mal an, eine Funktion f(x) soll symmetrisch zum Punkt P(1|2) sein. Wenn man diese Funktion um 1 nach links verschiebt und dann um 2 nach unten, müsste die neue, verschobene Funktion [ich habe sie f*(x) genannt und gestrichelt dargestellt] symmetrisch zum Ursprung sein. [Diese Symmetrie zum Ursprung könnte man dann über f(-x)=-f(x) beweisen].

Beispiel h.
f(x) = x³–6x²+9x–5
Zeigen Sie: f(x) ist zum Punkt S(2|-3) symmetrisch!
Lösung:
Wir zeigen das so: Zuerst verschieben wir f(x) um 2 nach links, dann um 3 nach oben.
Jetzt müsste der Symmetriepunkt im Ursprung liegen.
f*(x) = f(x+2) + 3 =
= (x+2)³ – 6(x+2)² + 9(x+2) – 5 + 3 = ... =
=(x³+6x²+12x+8)–6·(x²+4x+4)+9x+18–5+3 =
= x³+6x²+12x+8–6x²–24x–24+9x+18–5+3 =
= x³ – 3x
Man verschiebt eine Funktion um 2 nach links, indem man jedes „x“ der Funktion f(x) durch „(x+2)“ ersetzt.
Man verschiebt eine Funktion um 3 nach oben, indem man hinter die Funktion noch ein „+3“ dran hängt.
(siehe auch [A.23.01] Verschieben von Funktionen )
Die erhaltene Funktion f*(x)=x³–3x ist symmetrisch zum Ursprung, da sie nur ungerade Hochzahlen enthält. [Den Beweis über f(-x)=-f(x) brauchen wir gar nicht!]
Die Ausgangsfunktion ist f(x) symmetrisch zu S(2|-3)!
Beispiel i.
ft(x) = 0,6t·(6x+x²)
Zeigen Sie, dass ft(x) zur Geraden x=-3 symmetrisch ist!
Lösung:
Wenn f(x) symmetrisch zu x=-3 ist, können wir f(x) um 3 nach rechts verschieben, dann ist die verscho bene Funktion f*(x) symmetrisch zu x=0 [y-Achse].
f*(x) = f(x–3) = 0,6t·[ 6(x–3) + (x–3)² ] =
= 0,6t·[ 6x–18 + x²–6x+9 ] = 0,6t·[ x²–9 ]
Man verschiebt eine Funktion um 3 nach rechts, indem man jedes „x“ der Funktion f(x) durch „(x–3)“ ersetzt.
(siehe auch [A.23.01] Verschieben von Funktionen )
Die neue, verschobene Funktion hat nur gerade Hochzahlen in x. Sie ist also symmetrisch zur y-Achse.
Spaßeshalber können wir noch den richtigen Beweis durchführen:
f*(-x) = f*(x)
0,6t·[(-x)²–9] = 0,6t·[x²–9]
0,6t·[x²–9] = 0,6t·[x²–9]
wahre Aussage ⇒ Symmetrie ist bewiesen.
Beispiel j.

A.17.05 Symmetrie von Ableitungen
Wenn eine Funktion symmetrisch ist, zeigt sowohl ihre Ableitung, als auch ihre Stammfunktion ebenfalls Symmetrieeigenschaften auf.
Symmetrie von Ableitungen:
Ist eine Funktion f(x) symmetrisch zum Ursprung, dann ist ihre Ableitung f'(x) symmetrisch zur y-Achse.
Ist eine Funktion f(x) symmetrisch zur y-Achse, dann ist ihre Ableitung f'(x) symmetrisch zum Ursprung.
Symmetrie von Stammfunktionen:
Ist eine Funktion f(x) symmetrisch zum Ursprung, dann ist ihre Stammfunktion F(x) symmetrisch zur y-Achse.
Ist eine Funktion f(x) symmetrisch zur y-Achse, dann ist ihre Ableitung F(x) symmetrisch zu irgendeinem Punkt der y-Achse. [also nicht unbedingt zum Ursprung!]
Beispiel k.
Sei f(x) = 6x³+14x
f(x) ist punktsymmetrisch zum Ursprung, da nur ungerade Hochzahlen vorkommen. In der Ableitung f'(x) = 18x²+12 kommen nur gerade Hochzahlen vor, f'(x) ist also achsensymmetrisch zur y-Achse.
In der Stammfunktion F(x) = 2x4 + 7x² kommen ebenfalls nur gerade Hochzahlen vor, die Stammfunktion ist also auch achsensymmetrisch...


