Oberstufe

A.19 | Funktionsanalyse / Kurvendiskussion Beispielaufgaben

Unten finden Sie ausführliche Beispielaufgaben zur Kurvendiskussion. Alle Teilaufgaben der Funktionsanalyse werden einzeln erklärt: Ableitungen, Nullstellen, Extrema, Wendepunkte bis zum Schaubild der Funktion.

Außerdem finden Sie ausführliche, von unserem Gastdozenten Dr. Albus verständlich erklärte Übungsaufgaben-Videos hier.

Der Sinn der Funktionsanalyse ist es, die wichtigsten Eigenschaften einer Funktion zu errechnen.
Zu diesen gehören: Nullstellen, Hochpunkte, Tiefpunkte, Wendepunkte und asymptotisches Verhalten.

Zur Kurvendiskussion gehört:

⇒ Bildung von drei Ableitungen [braucht man für Extrempunkte und Wendepunkte].

⇒ Untersuchung der Funktion auf Achsensymmetrie bzw. Punktsymmetrie.

⇒ Untersuchung der Funktion auf asymptotisches Verhalten. [Wohin geht die Funktion, wenn x gegen +∞ oder -∞ läuft?]

⇒ Bestimmung der Nullstellen der Funktion [also Schnittpunkte mit der x-Achse].
Hierfür setzt man die Funktion gleich Null und löst nach „x“ auf. [Der Schnittpunkt der Funktion mit der y-Achse ist auch ganz nett, jedoch nicht so wichtig].

⇒ Bestimmung der Extrempunkte der Funktion [also Hoch- und Tiefpunkte].
Hierfür setzt man die erste Ableitung Null und löst nach „x“ auf. Die erhaltenen x-Werte setzt man zweimal ein: zum einen in f(x) um die y-Werte zu erhalten und zum anderen in f''(x), um zu schauen, ob es sich beim Punkt um einen Hoch- oder Tiefpunkt handelt. [Ist das Ergebnis von f''(x) negativ, so handelt es sich um einen Hochpunkt. Ist f''(x) positiv, so handelt es sich um einen Tiefpunkt. Ist das Ergebnis von f''(x) Null, so muss man f'(x) auf Vorzeichenwechsel untersuchen.]

⇒ Bestimmung der Wendepunkte der Funktion.
Hierfür setzt man die zweite Ableitung Null und löst nach „x“ auf. Die erhaltenen x-Werte setzt man zweimal ein: einmal in f(x) um die y-Werte zu erhalten und das zweite Mal in f'''(x), um zu beweisen, dass es sich tatsächlich um einen Wendepunkt handelt. [Ist das Ergebnis von f'''(x) nicht Null, so handelt es sich tatsächlich um einen Wendepunkt. Kommt doch Null raus, muss man f''(x) auf Vorzeichenwechsel untersuchen.]

⇒ Zeichnung der Funktion. [Eventuell mit Wertetabelle]

Schematische Darstellung der Funktionsanalyse:

⇒ Ableitungen: im Normalfall drei Stück

⇒ Symmetrie: Symmetrie zum Ursprung oder zur y-Achse ?!?

⇒ Asymptoten: senkrechte?? oder waagerechte bzw. schiefe?

⇒  Nullstellen:   f(x) = 0
               ⇒   man erhält    x1 , x2 , …
               ⇒   N1(x1|0) , N2(x2|0) , ..

⇒ Extrempunkte: f'(x) = 0 ⇒ x1 , x2 , …

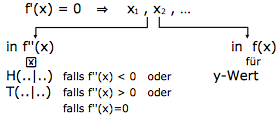
f'(x)=0 setzen
Die erhaltenen x-Werte, setzt man zum einen in f''(x) ein. [Falls das Ergebnis positiv ist, gibt's einen Tiefpunkt, falls es negativ ist, hat man einen Hochpunkt.]
Zum anderen setzt man die x-Werte nochmal in f(x) ein, um die y-Werte zu erhalten.

⇒ Extrempunkte: f'(x) = 0 ⇒ x1 , x2 , …

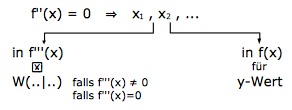
f''(x)=0 setzen
Die x-Werte, die man erhält, setzt man zum in f'''(x) ein. [Falls nicht Null rauskommt, ist es sicher ein Wendepunkt.]
Die x-Werte setzt man nochmal ein. Und zwar in f(x), um die y-Werte zu erhalten.

Falls bei der Überpru?fung der Extrem- oder Wendepunkte Null rauskommt, weiß man nicht ob hier Extrem- ein Wendepunkte vorliegen. Oft ist es ein Wendepunkt mit waagerechter Tangente. [Dieser heißt dann Terassenpunkt oder Sattelpunkt]. In diesem Fall muss man eine Untersuchung auf Vorzeichenwechsel vornehmen. Oder einfach die Skizze / Zeichnung angucken.
Siehe dazu Beispiel a.

Kurvendiskussion / Funktionsanalyse Beispiel a.

Untersuchen Sie f(x) ohne Verwendung eines grafik fähigen Taschenrechners auf Nullstellen, Extrempunkte, Wendepunkte, Symmetrie und Asymptoten. Fertigen Sie eine Zeichnung.

Lösung:

Ableitungen

Symmetrie
Es tauchen gerade und ungerade Hochzahlen auf       ⇒       das heißt: keine Symmetrie

Asymptoten
[Ganzrationale Funktionen haben keine Asymptoten.]
Verhalten für x→±∞ :        x→±∞       ⇒       f(x) → +∞
                                       x→±∞       ⇒       f(x) → -∞

Nullstellen

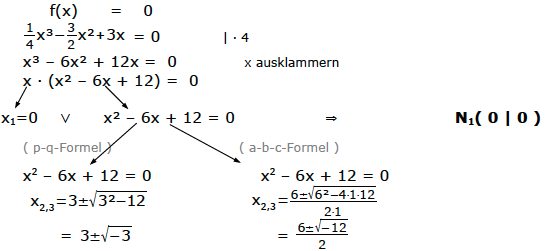
Da etwas Negatives unter der Wurzel auftaucht, gibt es keine weitere Lösung außer x₁=0.
Damit gibt es nur die eine Nullstelle N₁(0|0)

Extrempunkte

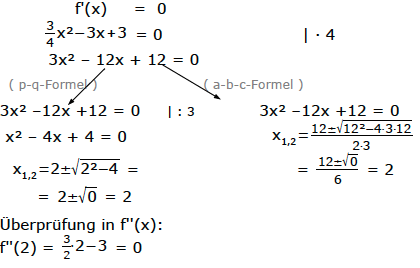
Wir merken uns, dass es sich bei x=2 um einen Sattelpunkt handeln könnte.
Später, bei der Berechnung der Wendepunkte, verwenden wir das.

In der zweiten Ableitung sollte nie Null rauskommen.
Wegen f''(2)=0 haben wir hier also ein Problem.
Wir wissen nicht, ob es sich bei x=2 um einen Hoch-, Tief- oder Wendepunkt handelt.
Wir brauchen eine Überpru?fung auf Vorzeichenwechsel.

Auf Vorzeichenwechsel überprüfen geht so:
Ausgangslage: Es ist zu überprüfen, ob bei einem bestimmten x-Wert (nennen wir diesen x=a) ein Hoch-, ein Tiefpunkt oder keines der beiden vorliegt.

Man betrachtet zwei x-Werte:
einen der kleiner als „a“ ist und einen der größer als „a“ ist.
Beide x-Werte setzt man in f'(x) ein und betrachtet die erhaltenen Vorzeichen.

Erhält man beim kleineren x-Wert was Positives und beim größeren was Negatives, befindet sich bei x=a ein Hochpunkt.

Erhält man beim kleineren x-Wert was Negatives und beim größeren was Positives, befindet sich bei x=a ein Tiefpunkt.

Erhält man beide Male was Positives oder beide Male was Negatives, handelt es sich normalerweise um einen Sattelpunkt (bzw. Terassenpunkt) (das ist ein Wendepunkt mit einer waagerechten Tangente).

Konkret geht die Untersuchung in unserem Fall also so:
Uns interessiert, ob bei x=2 ein Extrempunkt vorliegt.
Wir suchen uns daher zwei x-Werte aus, von denen einer größer, der andere kleiner als 2 ist.

z.B. wählen wir x1=1 und x2=3.
Nun setzen wir diese beiden x-Werte in f'(x) ein:

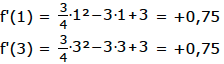
Wir erhalten beide Male ein positives Vorzeichen.
[der Wert „0,75“ spielt keine Rolle] ⇒ Bei x=2 liegt also kein Extrempunkt vor.

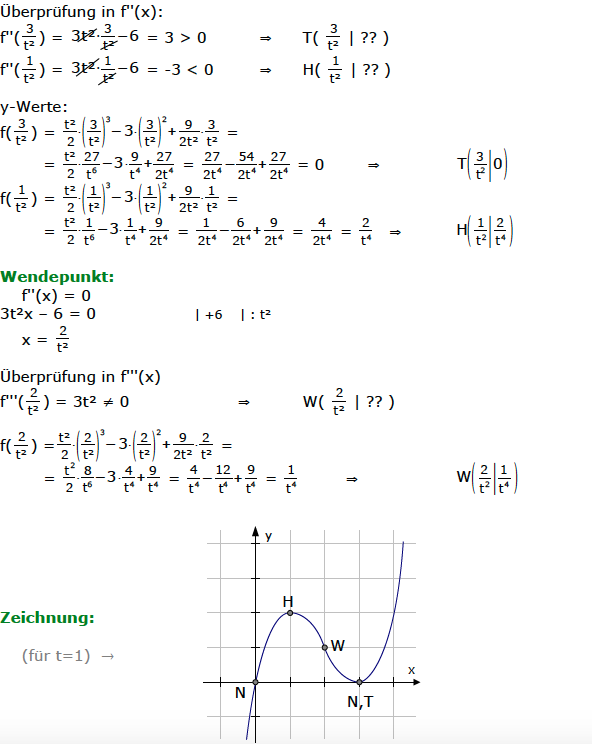
Wendepunkte

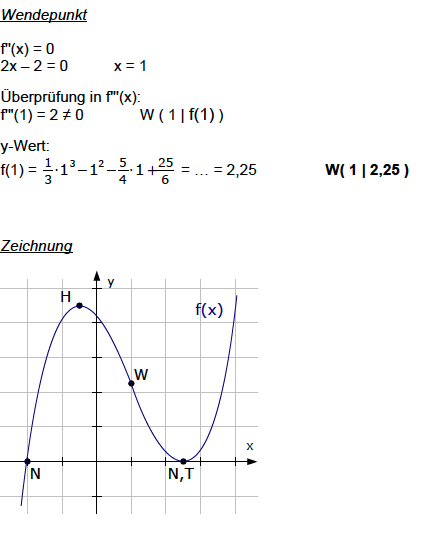
Bei der Berechnung der Extrempunkte erhielten wir f'(2)=0 (siehe Berechnung der Extrempunkte weiter oben). Dies bedeutet, dass bei x=2 die Steigung Null ist.
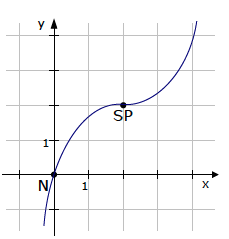
Im Punkt W(2|2) ist also ein Wendepunkt mit waagerechter Tangente.
Es handelt sich somit um einen Sattelpunkt! ⇒ SP( 2 | 2 )

Kurvendiskussion / Funktionsanalyse Beispiel b.

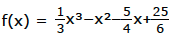
Zeigen Sie, dass f(x) bei N1(-2|0) und bei N2(2,5|0) Nullstellen besitzt.
Untersuchen Sie f(x) auf Extrem- und Wendepunkte, Symmetrie und Asymptoten.
Fertigen Sie eine Zeichnung.

Lösung:

Nullstellen
Wenn man die Nullstellen braucht, setzt man normalerweise f(x)=0 und löst nach x auf.
Hier jedoch sind die Nullstellen bereits gegeben.
Also setzen wir einfach die x-Werte in die Funktion ein und sollten als y-Wert „0“ erhalten.

Kurvendiskussion / Funktionsanalyse Beispiel c.

Für alle t∈?+ sei die Funktion ft(x) gegeben mit:

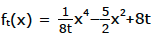
Untersuchen Sie die Kurvenschar ft(x) auf Nullstellen, Extrempunkte, Wendepunkte und Symmetrie.
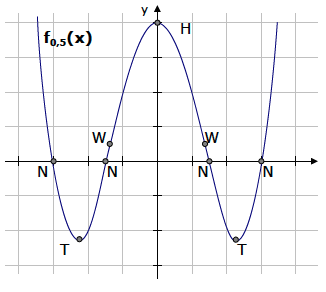
Fertigen Sie eine Zeichnung von f_0,5(x).

Lösung:
[t∈?+ bedeutet, dass der Parameter „t“ alle positiven Zahlen annehmen kann. Die „0“ ist in ?+ nicht enthalten!]

Info:

Am Anfang der Aufgabenstellung steht: t>0. Wäre das nicht angegeben, müsste man an dieser Stelle eine Fallunterscheidung machen, denn wenn t>0, dann gibt es bei "und" keine Probleme. Wäre jedoch t<0, dann wäre "und" gar nicht definiert. [Wurzel aus was Negativem gibt’s nicht]. Damit gäbe es für t<0 gar keine Nullstelle.