Oberstufe

A.11 | Was bedeutet f, f', f'', F, ...?

In der Analysis haben die verschiedenen Funktionen verschiedene Bedeutungen. Je nachdem wo man „x“ einsetzt erhält man verschiedene anschauliche Bedeutungen.

f(x) = y-Wert
f'(x) = Steigung
f''(x) = Krümmung
F(x) = Flächeninhalt

 

[A.11.01] Die Funktion f(x)

Die Hauptfunktion f(x) gibt immer die y-Werte einer Funktion an.
Um einen y-Wert zu berechnen, muss man also den x-Wert in die Funktion f(x) einsetzen.
Man verwendet die Funktion f(x) auch um Nullstellen zu berechnen.
Bei anwendungsorientierten Aufgaben ist f(x) oftmals der Bestand.

f(x) = y-Wert f'(x) = Steigung f''(x) = Krümmung F(x) = Flächeninhalt

 

 

 

[A.11.02] Die erste Ableitung f'(x)

Die erste Ableitung f'(x) gibt immer die Steigung einer Funktion und damit auch die Steigung der Tangente an.
Will man also die Steigung m der Funktion [oder der Tangente] in einem bestimmten Punkt berechnen, muss man den x-Wert des Punktes, um welches es geht, in die Ableitung f'(x) einsetzen.
Setzt man die erste Ableitung Null [f'(x)=0], erhält man die Hoch- und Tiefpunkte einer Funktion.
Ist f'(x) positiv, ist die Funktion an der Stelle monoton steigend,
ist f'(x) negativ, ist die Funktion an der Stelle monoton fallend.
Bei anwendungsorientierten Aufgaben ist die Ableitung f'(x) die Änderung des Bestands, oder auch Wachstumsrate bzw. Geschwindigkeit.
Bei einer Zunahme [=positive Änderung] hat die Ableitung positive Werte, bei einer Abnahme [=negative Änderung] hat die Ableitung negative Werte.

 

 

 

[A.11.03] Die zweite Ableitung f''(x)

Die zweite Ableitung f''(x) gibt die Krümmung einer Funktion an.
Ist f''(x) negativ, so handelt es sich um eine Rechtskurve.
Ist f''(x) positiv, so handelt es sich um eine Linkskurve.
Setzt man die zweite Ableitung Null [f''(x)=0], erhält man die Wendepunkte einer Funktion.
Bei anwendungsorientierten Aufgaben hat f''(x) normalerweise keine anschauliche Bedeutung.

 

 

 

[A.11.04] Die Stammfunktion F(x)

Die Stammfunktion [umgangssprachlich nennt man die Bildung der Stammfunktion auch „aufleiten“] benötigt man, um Flächeninhalte bzw. Integrale zu berechnen.

 

 

 

[A.11.05] Die Definitionsmenge

Die Definitionsmenge besteht aus allen x-Werten, die man in eine Funktion einsetzen darf.
Bei normalen Funktionen ist die Definitionsmenge immer die Menge der reellen Zahlen (D= R), die Def.menge besteht also normalerweise aus allen Zahlen.
Falls eine Funktion irgendwo im Nenner [also unter´m Bruchstrich] ein „x“ enthält, macht die Definitionsmenge Probleme. In diesem Fall muss man den Nenner Null setzen und die erhaltenen x-Werte aus D ausschließen.
Bsp:   

Falls eine Funktion irgendwo eine Wurzel enthält, macht die Definitionsmenge ebenfalls Probleme. In diesem Fall muss der Term unter der Wurzel positiv sein.
Bsp: 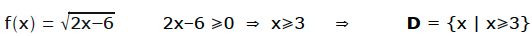           andere Schreibweise wäre: D = [ 3 ; + ∞ ]

 

 

 

[A.11.06] Die Wertemenge

Die Wertemenge, besteht aus allen y-Werten, die eine Funktion annehmen kann.
Der beste Weg, die Wertemenge zu erhalten, ist eine Zeichnung von f(x) zu machen und dann anhand von Hoch- und Tiefpunkten sowie Asymptoten [wohin geht die Funktion, woher kommt sie] zu schauen, was für y-Werte auftauchen können.

 

Bsp: f(x) = -2x³+4x²–5

f(x) läuft von oben (+∞) bis unten (-∞). Es tauchen also alle y-Werte auf.   ⇒   W=R.

Bsp: g(x) = 0,5x⁴– 2x²

g(x) läuft hoch bis +∞. Nach unten jedoch nur bis y=-2, was man an den y-Werten der Tiefpunkte sieht.   ⇒   W = { y | y >= -2 } ()

 

 

 

 

[A.11.07] Monotonie

Eine Funktion ist monoton steigend (monoton wachsend), wenn die Steigung immer positiv oder Null ist bzw. wenn die erste Ableitung immer positiv oder Null ist.
Eine Funktion ist streng monoton steigend (streng monoton wachsend), wenn die Steigung immer positiv ist bzw. wenn die erste Ableitung immer positiv ist.
Eine Funktion ist monoton fallend (monoton abnehmend), wenn die Steigung immer negativ oder Null ist bzw. wenn die erste Ableitung immer negativ oder Null ist.
Eine Funktion ist streng monoton fallend (streng monoton abnehmend), wenn die Steigung immer negativ ist bzw. wenn die erste Ableitung immer negativ ist.

Bemerkung:
Falls man an der Ableitung f'(x) nur schwer erkennen kann, ob diese für die gewünschten x-Werte positiv oder negativ ist [und f(x) damit steigend oder fallend], berechnet man einfach Hoch- und Tiefpunkte der Funktion. In einem Bereich rechts vom HP und links vom TP ist eine Funktion logischerweise (streng) monoton fallend. In einem Bereich rechts vom TP und links vom HP ist eine Funktion logischerweise (streng) monoton steigend.

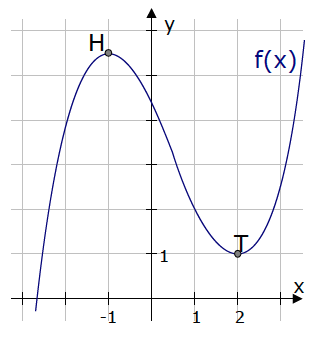
Zur Skizze unten:
Für x < -1 ist f(x) streng monoton steigend.
Für x <= -1 ist f(x) monoton steigend.
Für -1 < x < 2 ist f(x) streng monoton fallend.
Für -1 <= x <=  2 ist f(x) monoton fallend.
Für x > 2 ist f(x) streng monoton steigend.
Für x >= 2 ist f(x) monoton steigend.

Bsp:
Zeigen Sie, dass f(x) = 2(1–3x³)⁵ monoton ist.

Lösung:
Wir betrachten die Ableitung f'(x)   >>>   f'(x) = 2·5·(1–3x³)⁴·(-9x²) ⇒ f'(x) = -90x²·(1–3x³)⁴
f'(x) ist negativ, da „-90x²“ negativ ist [Quadrate sind positiv] und die Klammer positiv ist [die gerade Hochzahl macht die Klammer positiv]. Da Plus mal Minus ein negatives Ergebnis liefert, muss f'(x) also negativ sein!    f(x) ist also monoton fallend!

 

 

 

[A.11.08] Krümmungsverhalten

Wird nach dem Krümmungsverhalten gefragt, möchte man wissen, ob die Funktion linksgekrümmt oder rechtsgekrümmt ist.

Linkskrümmung: f''(x)>0 Rechtskrümmung: f''(x) < 0

Eine Funktion ist linksgekrümmt, wenn die zweite Ableitung positiv ist.
Eine Funktion ist rechtsgekrümmt, wenn die zweite Ableitung negativ ist.
Um Links- oder Rechtskrümmung bei einer Funktion zu unterscheiden, beginnt man am linken Rand der Skizze, stellt sich vor, dass die Kurve eine Straße ist, auf die man von oben schaut.
Wenn man nun auf der Straße so gemütlich entlangfährt und das Lenkrad nach links dreht hat man eben eine Linkskurve, anderenfalls eben eine Rechtskurve.
Die Grenze zwischen eine Rechts- bzw. Linkskurve ist immer ein Wendepunkt.

Zur Skizze unten:
Für x < -1,5 [links vom linken Wendepunkt] ist f(x) linksgekrümmt.
Für -1,5 < x < 1,5 [zwischen den Wendepunkten] ist f(x) rechtsgekrümmt.
Für x > 1,5 [rechts vom rechten Wendepunkt] ist f(x) wieder linksgekrümmt.

Bsp:
In welchem Bereich ist f(x) = x³–6x²+3x–1 linksgekrümmt?

Lösung:
Wir brauchen die zweite Ableitung:    f'(x)=3x²–12x+3    ⇒    f''(x)=6x–12
f(x) ist linksgekrümmt, wenn f''(x) > 0   ⇒    6x–12 > 0         |+12    |:6
x > 2

Antwort:    für x>2 ist f(x) rechtsgekrümmt!